Option pricing using Monte Carlo Simulation In our post on Option Pricing using Monte Carlo Simulation, we walk through a simple modeling framework used for pricing vanilla as well as exotic options in Excel. After the framework is introduced we drop a few hints on how to price Asian, Barrier, Ladder & Chooser options using Monte […]
Exotic derivatives & Options pricing – Pricing Chooser and Compound Options – Weekend Challenge
Exotic Derivatives & Option pricing weekend challenge This week exotic option pricing challenge focuses on chooser and compound option pricing using Monte Carlo Simulation in Excel. Hints to the solution will be posted separately within the next 12 hours. Let’s see if you can crack this first before I go ahead and post the solved solution. […]
Delta Hedging & Option Greeks – Quant Interview Study Guide
Understanding Delta Hedging & Greeks – Technical Interview Guide
Till November 30th, take $60 off the cover price when you order your electronic copy. The package include a 71 page study guide and 3 supplementary Excel Spreadsheets that focus on Monte Carlo Simulation of Dynamic Delta Hedging, Calculation of Cash PnL & Dissection of Option Price Sensitivities (Greeks).
Learn more about the title through the Delta Hedging & Greeks Book launch post.
Sales & Trading Interviews – Understanding Greeks & Delta Hedging – Now in Stores
Technical Sales & Trading Interviews – Understanding Greeks & Delta Hedging
Delta Hedging – Designed for audiences with:
- Job Interviews with Sales & Trading, Risk Management or Quantitative Strategies Desks.
- Deadlines for building, tweaking an inhouse dynamic delta hedging model for internal reporting, analysis and discussion.
- Training classes with fresh intake or interns who need to learn the ropes as of yesterday.
- Educating clients & bosses by testing and simulating scenarios cutting across strikes, spots, volatility, rates and time to expiry.
What does it include:
- A Delta Hedging Excel Monte Carlo simulation using our step by step, easy to follow, guide.
- A guide to Simulating Cash PnL for hedging your European Call & Put Exposure
- An analysis of PnL relationships and Option price sensitivities (Greeks)
- Plots of Greeks against changing spot, strike, volatility, expiry & interest rates.
And
- A downloadable 70 page PDF guide for building the Delta Hedging Monte Carlo Simulation in Excel.
- A Greeks suspects gallery for common plots of Delta, Gamma, Vega, Theta & Rho.
- Step by step cash PnL calculation for a Call Option.
- A dissection of Delta, Gamma, Vega, Theta & Rho that doesn’t rely on the formula but uses graphs, intuition and thought experiments.
Understanding Greeks and Delta Hedging – Origins
What started off as a study note to address an intelligent question from a student and completely inadequate teaching on my part, turned into a monster side project that consumed the best part of a year.
The original question dealt with the behavior of Greeks, usage of higher order Greeks by traders and the concept of Delta hedging. It was supplemented by a request for recommended reading that I would care to suggest on this topic.
The challenge was that other than Nassim Taleb’s Dynamic Hedging there is literally nothing out there that you could refer a curious soul to. While Dynamic Hedging is the one and only guide on this topic, it generally leads to Cardiac infractions and CVA’s (Cerebrovascular Accident, not Credit Value Adjustments) in new students. To reduce mortality rate of fresh intakes in computational finance graduate programs and sales and trading desks, there was need for a beginners guide. Ideally with no stochastic calculus and no partial differential equations.
The end result: A study guide that walks through Option Price Sensitivities and Greeks behavior, helps you plot the same in Excel, use a dynamic Delta hedging simulation to get you comfortable with the majors and uses a Cash PnL simulation to dissect the minor Greeks.
It is not a conventional interview guide with interview questions. More like a survival kit that you can use to brush up on Greeks in a rush before the interview or before your exam. You don’t want to digest Taleb the night before; but you can play with an Excel sheet and tweak it to till you are able to connect the missing dots.
The complete package includes a 73 page study note and 3 Excel spreadsheets that you can cover end to end in about 3 hours and build intuition that can help you navigate trick questions and traps in the interview room.
Pick a copy under the early buyers promotion valid till 3oth November and take $60 dollars off the cover price.
Understanding Option Greeks – Free Sample content
The problem with Greeks is that the topic is so out there for most students and non-practitioners that we would rather ignore it. Who would actually care about the second moment (Gamma) or the third (Delta of Gamma) for that matter in the non-trading desk world. Plus by the time you actually get to a level that you can talk intelligently about the subject you are so short of oxygen that there is nobody left to talk to.
Understanding Greeks – Introduction
Understanding Greeks – Analyzing Delta & Gamma
Understanding Greeks – The Guide to delta hedging using Monte Carlo Simulation
Dynamic Delta Hedging Simulation – Cash PnL calculations
Using Dynamic Delta Hedging Simulation as a learning tool
Understanding Greeks – Quick Reference Guide to Delta, Gamma, Vega, Theta & Rho
Understanding Greeks & Delta Hedging – Motivation
I remember the pain I went through when I first tried to decipher Greeks, Continuous Time Finance and Monte Carlo Simulations. It was only when I met Mark Broadie and Maria Vassalou at Columbia that the cobwebs in my mind cleared up. While this book doesn’t deal with the original pain, it uses the approach Mark used to teach us a fairly difficult subject. Use Excel, Monte Carlo Simulation and intelligent questions (aka thought experiments).
The book is therefore packaged with spreadsheets that can be used interactively with relevant sections (see included Excel spreadsheets detail specification at the end of this post). As a student you can actually build the sheets using the step by step guides or simply use the packaged editions to answer the questions we ask.
And we ask many questions. In fact in one specific section we lead you all around town using the incorrect approach till you finally figure out the right answer. I have found this to be one of the most effective ways of ensuring comprehension and understanding.
The 73 pages are primarily a guide to building a delta hedging spreadsheet for European Call and Put Options. Nassim Taleb emphasizes the use of a generator function to build trader intuition and we have included one. We then use the Delta hedging sheet to think about Delta, Gamma, Vega & Rho by asking questions that help reinforce that intuition. For Greeks we include an Excel calculation spread sheets as well as over thirty graphs that analyze Greeks behavior across changing Spot, Strikes, Volatility, Time & Interest rates.
To get the most out of the package, we recommend that you follow the book and the templates to build your Excel spreadsheets from scratch.
However the most important section of the book deals with Cash PnL from dynamic hedging. It turns out to be a terrific tool, once you link the profitability calculation to Greeks and use it to dissect components and contributors to PnL.
The Table of Content produced below has more details.
Pick a copy under the early buyers promotion valid till 30th November and take $60 dollars off the cover price.
Dynamic Delta Hedging – Monte Carlo Simulation – Greeks – Downloadable Excel File Guide
This product contains 3 EXCEL files.
1. Option Greeks Calculation & Graphs
- Calculation of the Black Scholes option price for a European Call and a European Put option
- Calculation of Greeks- Delta, Gamma, Vega, Theta & Rho- for a European Call and a European Put option
- Data table that captures the Black Scholes risk adjusted probabilities and option premium across a series of volatilities
- Graphical representation of Black Scholes risk adjusted probabilities and option premium against volatilities
- Data tables that capture the sensitivity of the Greeks against Spot, Strike, Time to maturity, Volatility and the Risk Free Rate respectively
- Graphical representation of the sensitivities of the various Greeks against Spot, Strike, Time to maturity, volatility and risk free rate respectively
2. Dynamic Delta Hedging – Call Option – Monte Carlo Simulation – Cash PnL
- Calculation of a 12-step Monte Carlo simulation model that generates the underlying stock price series
- Calculation of theoretical option values using the Black Scholes call option price formula
- Calculation of call option deltas at each rebalancing interval
- Calculation of a replicating portfolio that consists of a long position in Delta times the stock and a short position in the amount borrowed (net of the option premium received at inception) to fund the initial & subsequent incremental purchases
- Graphical representation of the theoretical option value and the replicating portfolio value over the life of the option
- Calculation of a tracking error for the difference between the value of the replicating portfolio and the theoretical value of the option
- Graphical representation of the tracking error across the life of the option
- Determination of the per period interest and principal portions of the amount borrowed
- Determination of the Gain (Loss) on sale of portions of the stock
- Setting up a Cash Accounting P&L that shows cash inflows from option premium received and strike received in the event the option is exercise and cash outflows from interest and principal repayment on the amount borrowed
- A choice of including of excluding the option premium in determining the amount borrowed at inception. In this case the Principal repaid will equal the gain (loss) if the option is not exercised.
- 100 simulated runs including a graphical depiction of the results showing the Net P&L, Amount borrowed (principal & interest) and Gain/ Losses; and averages across the 100 runs for each of these items
3. Dynamic Delta Hedging – Put Option – Monte Carlo Simulation – Cash PnL
- Calculation of a 12-step Monte Carlo simulation model that generates the underlying stock price series
- Calculation of theoretical option values using the Black Scholes put option price formula
- Calculation of put option deltas at each rebalancing interval
- Calculation of a replicating portfolio that consists of a short sale of Delta times the stock and lending of the initial (net of the option premium received at inception) & subsequent incremental short sales proceeds
- Graphical representation of the theoretical option value and the replicating portfolio value over the life of the option
- Calculation of a tracking error for the difference between the value of the replicating portfolio and the theoretical value of the option
- Graphical representation of the tracking error across the life of the option
- Determination of the per period interest and principal portions of the amount lent
- Determination of the Gain (Loss) on closing of short sale positions
- Setting up a Cash Accounting P&L that shows cash inflows from option premium received, interest earned on amount lent and sales proceeds from short sales and cash outflows from strike paid if the option is exercised
- A choice of including or excluding the option premium in determining the amount borrowed at inception. In this case the sales proceeds from short sales will equal the gain (loss) if the option is not exercised.
- 100 simulated runs including a graphical depiction of the results showing the Net P&L, Proceeds from Short Sales, Interest Earned and Gain/ Losses; and averages across the 100 runs for each of these items
Pick a copy under the early buyers promotion valid till end of November and take $60 dollars off the cover price.
Related posts:
Delta Hedging applications for Rho, Rebalancing frequency & Implied Volatility
Rebalancing frequency, Implied Volatility & Rho. Dynamic Delta Hedging Applications.
Now that we have a Delta Hedging Model for Calls and Puts let’s try and use it to answer the following questions:
a) What is the impact of rebalancing frequency on hedging profitability?
b) What is the impact of a rise in volatility on profitability? How does implied volatility help in interpreting this change?
c) What is the impact of changes in risk free rates on profitability?
d) How does the interaction of time to expiry and volatility changes profitability?
These are all questions that should occur naturally to you as you spend more time with the Delta Hedging model. They are also essential to building a deeper understanding of the concept of implied volatility, Rho & Theta.
Dynamic Delta Hedging Questions: Assumptions & Securities
Let’s take a look at these questions one by one. We will begin work with a call option assuming the following valuation parameters:
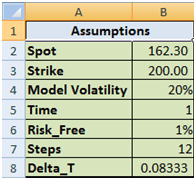
Figure 1 Dynamic Delta Hedging – P&L review assumptions
The theoretical value of the call option is 3.01 based on the above assumptions. The resulting Cash Accounting P&L for a single run of the Dynamic Delta Hedging model is as under:
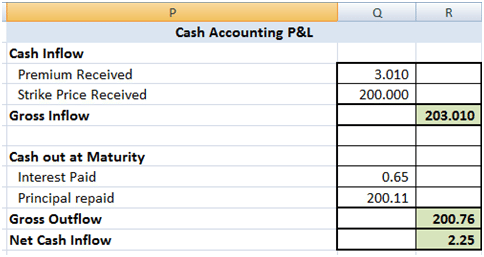
Figure 2 Dynamic Delta Hedging – P&L Review – Base case
Rebalancing frequency & efficiency of the hedge. Implications for profitability?
A good hedge is one where the cost of the hedge is close to the theoretical value of the option. In our cash accounting P&L we have included the theoretical premium received which is used in determining the initial amount to be borrowed. Hence for a hedge to be considered good or efficient the Net P&L should be close to this premium amount.
To see if increasing the frequency led to better results, we increase the time steps used from 12 steps to 365 steps. The graph below plots the Net P&L to Theoretical Value across 100 simulated runs. A value close to 100% means that it is a close match to the premium whereas a value farther away for 100% indicates a poor match.
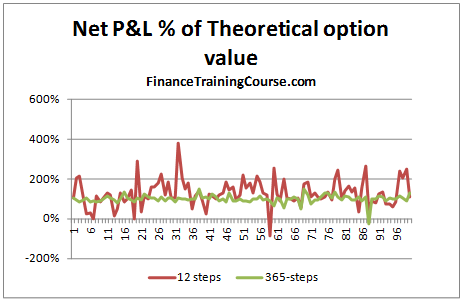
Figure 3 Dynamic Delta Hedging – P&L Simulation – Rebalancing frequency
We can clearly see that there is much greater variation when the rebalancing is done on a monthly basis than when it is carried out on a daily basis.
The graph below gives a similar picture. In this case however, the premium is not considered when determining the amount to be borrowed at option inception, i.e. the hedge is fully funded through borrowing. A value of -100% indicates that the Net P&L i.e. the cost of the hedge, in this case exactly matches the theoretical value of the call option.

Figure 4 Dynamic Delta Hedging – P&L Simulation – Hedge Effectiveness
But that is the risk manager’s point of view. What about a trader’s point of view?
From a trading point of view there are two lessons here. First the large variation in P&L linked to jump’s in the underlying price is the un-hedged Gamma at work (Is that true? Think about it). Second would you prefer to limit the cost of hedging the option to the amount you have charged your customer or less? If you are in the business of earning a living from writing options, the premium you charge on the options you sell should always be higher than your cost; your cost of effectively hedging the option.
Now back to the Gamma question. Gamma is your second order error term. Conceptually it’s similar to convexity and linked to changes in not just the underlying price but also volatility. Is your true P&L (the premium received less the actual cost of hedging) is the summation of the hedge error?
Volatility and profitability. The question of implied volatility
With volatility there are multiple questions. How does profitability change when the general environment moves from low volatility to high volatility? How does profitability change when you have already written an option and volatility moves for or against you?
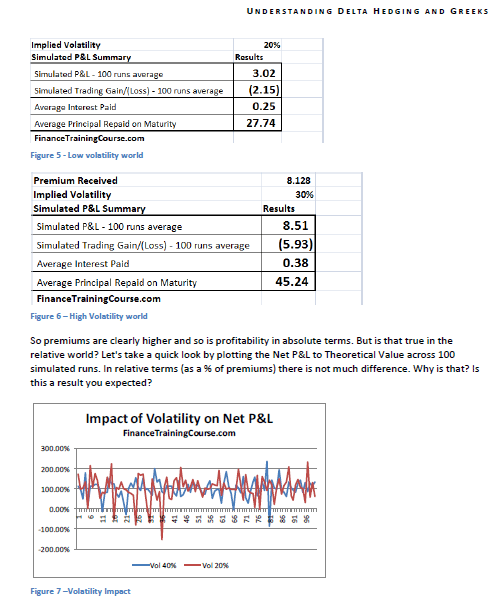
Let’s start from the first question. Using the 12-step model we calculate the impact on Net P&L. In our base case we have assumed a volatility of 20%. Let us now assume that the volatility increases to 40%. What is the impact on hedge efficiency for options written in the two different environment?

Figure 5 Volatility & Profitability – Low volatility world
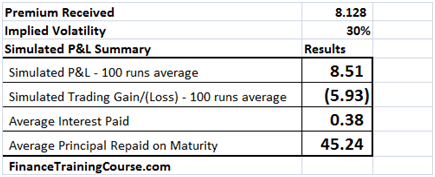
Figure 6 Volatility & Profitability – High Volatility world
So premiums are clearly higher and so is profitability in absolute terms. But is that true in the relative world? Let’s take a quick look by plotting the Net P&L to Theoretical Value across 100 simulated runs. In relative terms (as a % of premiums) there is not much difference. Why is that? Is this a result you expected?
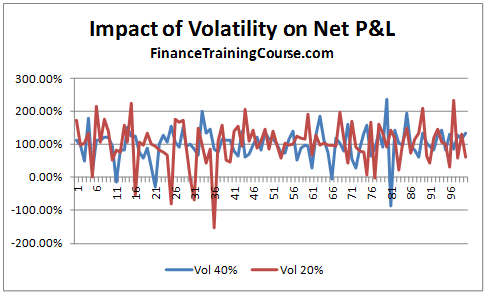
Figure 7 Dynamic Delta Hedging – P&L Simulation – Volatility Impact
To answer these questions you have to revisit implied volatility. Let’s use the same scenario as above but with a minor change. We wrote options and received premiums assuming an implied volatility of 30%. The actual realized volatility over the life of the option was 20%. How did that change our resulting simulated P&L.

Figure 8 Implied volatility at work – Hedge Profitability
You can now see a clear difference in absolute as well as relative terms in net P&L. And the difference arises on account of the spread between the premium charged ($8.13) versus the premium needed ($3.01).
(To run this exercise using the Delta Hedge Sheet, simply calculate the value of the premium at the implied volatility level you want to charge and replace the original premium in the simulation with this value).
Risk free rates & profitability. The question of Rho.
We present the results of three P&L simulations runs in the tables below. The first assumes a risk free interest rate of 1%, the 2nd uses 2% and the third uses a risk free interest rate estimate of 5%.
The first two are easy, rates go up, premiums goes up and a European Call option becomes more expensive. Why is that?
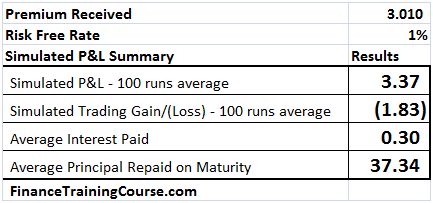
Figure 9 Dynamic Delta Hedging profitability – P&L at 1% interest rates
The reason is the average interest paid column. The premium goes up by 28 cents of which 21 cents is the increased cost of financing the borrowed position. Where does the other 7 cents comes from? (Need a hint – Other than the borrowing component who else benefits or uses r, the risk free rate?)
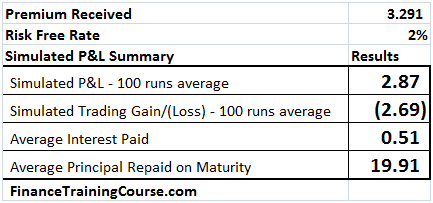
Figure 10 Dynamic Delta Hedging profitability – P&L at 2% interest rate
The second one is more difficult. In this instance as rates increase to 5% from the original 1%, the cost of borrowing balloons to $1.95 from the original $0.30 but the impact in option premium is only $1.244. How does this work? (Hint, think about what other driver/factor in the Black Scholes Analysis uses r?)

Figure 11 Dynamic Delta Hedging profitability – P&L at 5% interest rates
In addition to borrowing the difference between premium received and Delta hedge, the other usage of the risk free rate, r, is in estimating the future value of the underlying asset in the BSM (Black Scholes Model’s) risk neutral world. This implies that there are other components of Rho, in addition to the borrowing cost. That you need to examine and be comfortable with.
Related posts:
Hedging Gamma & Vega – The higher order Greeks hedge optimization Excel spreadsheet – Part I
Hedging Higher Order Greeks – Hedging Gamma & Vega using Microsoft Excel
In earlier posts we have set the foundation for hedging in practice. We did this by calculating Option Price Sensitivities (Greeks) and Delta hedging for European Call as well as Put Options.
Why would you want to hedge Gamma?
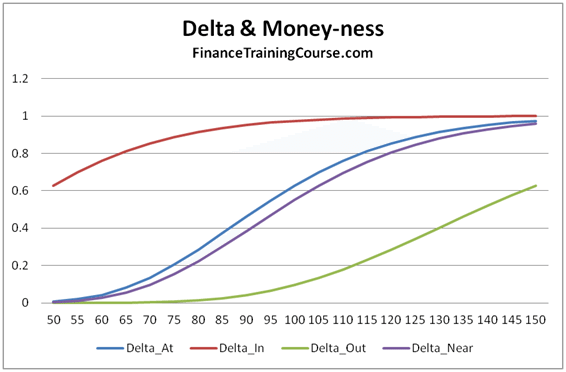
Figure 1 Options Greeks – Delta and Moneyness – Hedging higher order Greeks
If you leave it un-hedged you are exposed to the risk of large moves, especially when the option is at or near money. When you are deep out or deep in, Delta is flat and asymptotic as shown above. But when are you not, a large move can result in significant trading loss despite being Delta hedged. As long as prices move in small increments and do not jump dramatically, Delta hedge will cover you. The underlying jumps, you are exposed.
We have seen this at work earlier with duration and convexity with similar implications. Delta is the first order rate of change and works well within a narrow band. Within and outside that band Gamma tracks not just the error but also the magnitude of your gain/loss in case of a large move (up/down). The magnitude of the error shifts dramatically as the option gets closer to the At/Near money state. When options are deep in or deep out, similar to Delta, Gamma also flattens out. However given the convex nature of the 2nd derivative in this case, the impact of a large up move or a large down move is not symmetric.
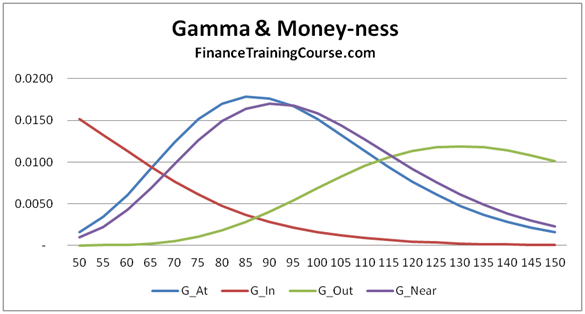
Figure 2 Option Greeks – Gamma & Moneyness – Hedging Higher order Greeks
But you can’t hedge higher order Greeks (Gamma) by buying or selling the underlying. Why not?
First the 2nd derivative of a spot/forward/linear position is zero so hedging Gamma through the underlying is out. The second complexity arises with Vega. We really don’t know what shape or form realized volatility will take in the future. How can we effectively hedge it?
Then there is the issue of term structure of volatility. Implied volatility changes based on time to maturity (term structure) as well as money-ness (deep in, deep out, At/Near – strike price) so taking a simple constant volatility view across all options irrespective of maturity or money-ness would actually be in-accurate.
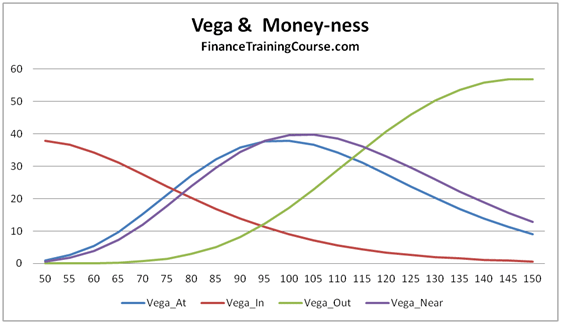
Figure 3 Option Greeks – Vega & Moneyness – Hedging higher order Greeks
The third catch is that both Gamma and Vega use exactly the same calculation function for Calls and Puts (Gamma for a call and put has the same value, Vega for a call and a put has the same value). Which creates interesting implications for hedging a book of options with calls and puts. You may be perfectly hedged and squared with respect to your Gamma and Vega exposures but the wrong universe/direction of hedging choices can still wipe you out.
We hedge Gamma and Vega by buying other options (specifically cheaper out of money options) with similar maturities. Like Delta hedging we need to rebalance but the rebalance frequency is less frequent than Delta hedging. Your final hedge is therefore a mix of exposure to the underlying (partial delta hedge) and cheaper options with similar maturities.
The only question is that it’s a large universe of options out there, how do we manage multiple constraints including premium & sensitivities across products, maturities (tenors), Delta, Gamma & Vega. The answer is constraint optimization through Excel solver. In our next post we will show how to build a simple Excel solver model that takes a universe of four options and uses it to match the required Delta, Gamma, Vega profile for a single option.
Before we jump to the next post, please review the following background posts on Option Greeks & Delta Hedging to ensure that you are comfortable with the calculation of Delta, Gamma & Vega as well the implementation of Delta Hedging in Excel.
Understanding Option Greeks – Relevant Sales & Trading Interview Guides posts
Understanding Greeks – Introduction
Understanding Greeks – Analyzing Delta & Gamma
Understanding Greeks – The Guide to delta hedging using Monte Carlo Simulation
Understanding Greeks – Quick Reference Guide to Delta, Gamma, Vega, Theta & Rho
Related posts:
Sales & Trading Technical Interviews – Greeks behaving badly – Put Options
Understanding Option Price Sensitivities – European Put Options – Sales & Trading Technical Interview Guides
As part of our Sales & Trading technical interview guide series we have done a number of posts on Greeks, Delta hedging and estimation of Delta hedging Profit & Loss.
A recent client/student/interview request indicated a preference/need for a sheet dedicated to European Put Options Greek plots. Hence the Greeks Put Option suspects’ gallery. While some of these are making a second appearance, we think a Put only collection is indeed useful given our focus on European Call options.
The Analysis framework used for dissecting put option Greeks is simple. We break the contracts down by “money-ness”. The three categories are Deep In, At/Near, Deep Out of money options.
And the five option pricing variables – Spot, Strike, Vol, Interest Rates & Time. This analytical combination produces interesting results.
The options for which Greeks have been plotted below assume a volatility of 20%, a risk free rate of 5% and a time to maturity of 1 year. In addition Spot and Strike prices are:
Deep In
Spot = 50
Strike = 100
At/Near
Spot = 50
Strike = 100
Deep Out
Spot = 50
Strike = 100
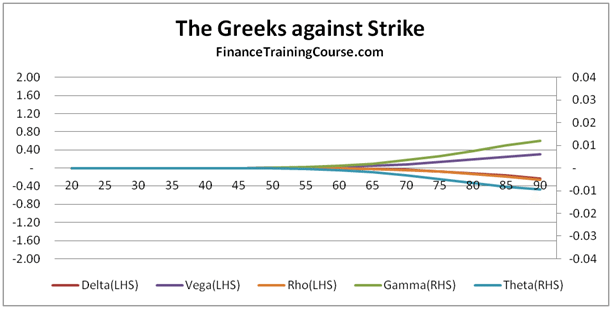
Greeks Against Spot – European Put Options
European Put Options – Deep In the money Options
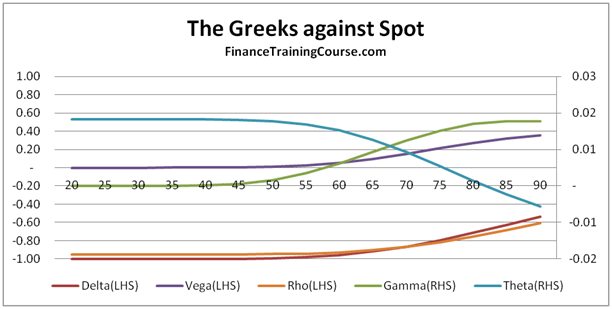
European Put Options – At/Near Money Options
European Put Options – Deep Out of money Options

Greeks Against Spot – European Put Options
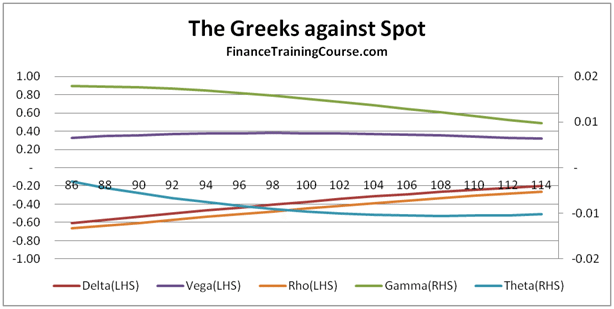
European Put Options – Deep In the money Options
European Put Options – At/Near money Options
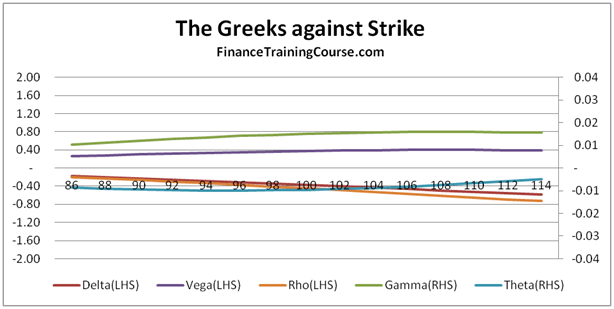
European Put Options – Deep out of money Options
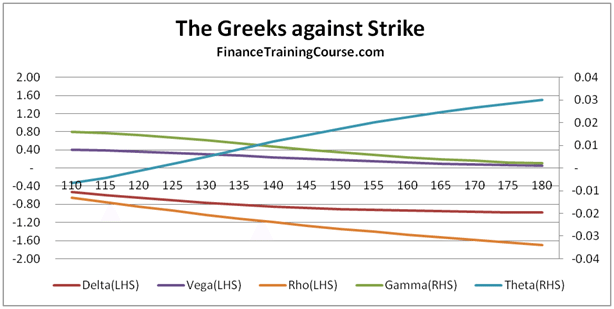
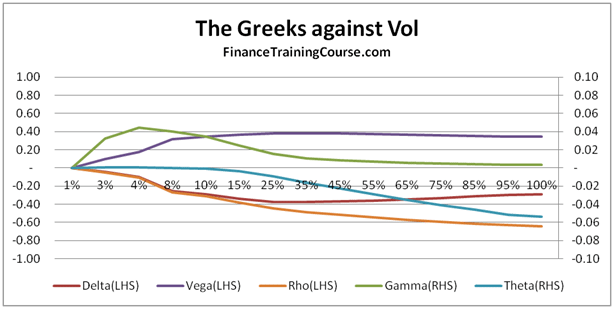
European Put Option Greeks – Against Volatility
European Put Options – At/In money Options
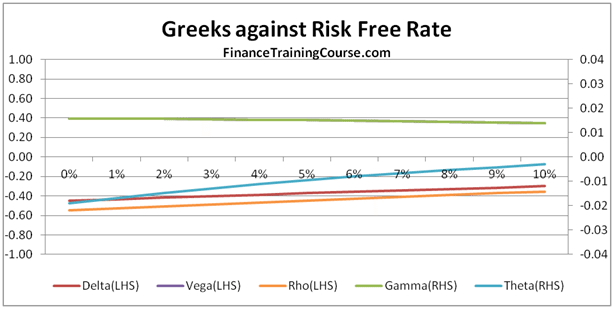
European Put Options – Against Changing Interest Rates
European Put Options – At/Near money Options
European Put Options – Against Changing Time to Maturity
European Put Options – At/Near money Options
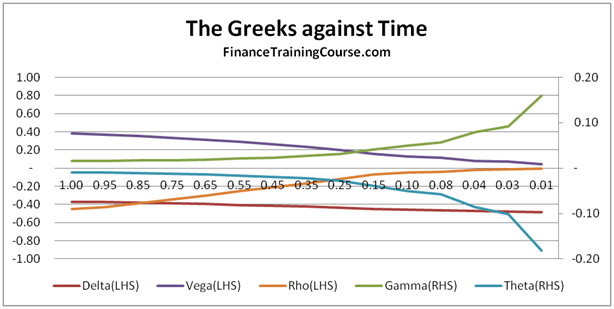
Understanding Option Greeks – Relevant Sales & Trading Interview Guides prior posts
Understanding Greeks – Introduction
Understanding Greeks – Analyzing Delta & Gamma
Understanding Greeks – The Guide to delta hedging using Monte Carlo Simulation
Understanding Greeks – Quick Reference Guide to Delta, Gamma, Vega, Theta & Rho
Related posts:
Keep a tab on the odds for the US Presidential election. Who is winning? A bet?
If you have been playing the odds game mentally for the US Presidential election and want a resource to take a bet on your view on the likely winner on 6th November 2012, here is an interesting resource.
The Intra-Trade US Presidential Election Prediction ticker. The 10 dollar par value share predicting a US Presidential election win for President Obama is now trading at $6.6 and change. Governor Romney is down at $3.3 per share. Pre-Sandy the range was $6.2 for President Obama and $3.7 for Governor Romney. If you buy now and the man from Chicago wins, your share will settle at $10 par, netting you a cool 50% return in 4 days.
Any takers?
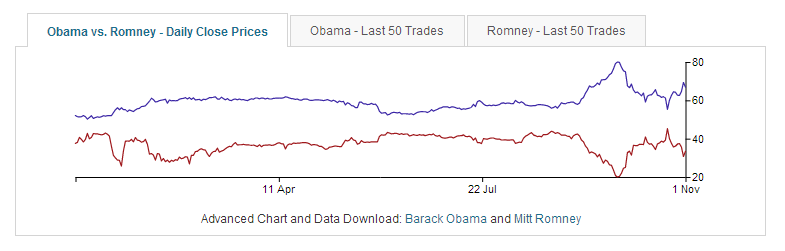
Take a quick look at the Campaign roundup by John Avlon at the Daily Beast before you take your position. John is predicting a close race but with the incumbent as the likely winner, based on early voting trends in Ohio where the spread between the two candidates is 26 points rather than the neck to neck finish Gallup is forecasting.
A big thanks to Rakesh Gopchandhani for sharing it.
Ps. For the Sharia compliant crowd, this is not an investment, it is a bet.
Related posts:
Dynamic Delta Hedging – Calculating Cash PnL (Profit & Loss) for a Call Option writer
Dynamic Delta Hedging – Calculating Cash PnL (P&L) for a European Call Option
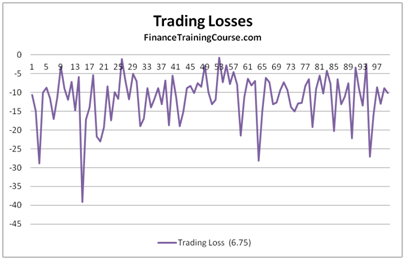
Figure 1 Delta Hedge P&L – Trading losses on account of rebalancing
We extend the original Dynamic Delta Hedging Monte Carlo Simulation spread sheet in this note. The dynamic hedging spreadsheet for a European call option allowed us to do a step by step trace of a delta hedging simulation. In this sheet we will use the results from the simulation trace to calculate a cash accounting P&L for our hedging model assuming the role of a call option writer and then extend the original simulation to see the average PnL across 100 iterations.
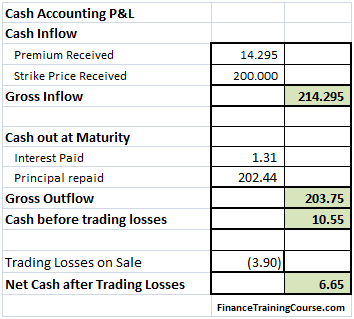
The above calculation has a double count in it? Which directly impacts the final profitability figure? Can you see it? See the discussion below for an answer.
We are assuming that we have written a European call option on Barclays Bank where the current spot price is $162.3 and the strike price is US$200. Time to expiry is one year and Barclays Bank is unlikely to pay a dividend during the life of the option.
Figure 2 Delta Hedge P&L – Cash P&L for the writer for a call option that expires in the money
Understanding Delta Hedging Cash PnL Calculation – Required resources
Before you proceed further if you are still uncomfortable with option price sensitivities or delta hedging please use the following background and model review posts to make yourself comfortable with the underlying concepts.
- Understanding option Greeks reference resource for dummies
- Understanding Greeks – Analyzing Delta & Gamma
- Understanding Greeks – The Guide to delta hedging using Monte Carlo Simulation
- Understanding Greeks – The Delta Hedging Simulation extended for Put Options
Delta Hedging Cash PnL Calculations – Dissecting the PnL Model
Our model uses a simplified cash based approach to calculate PnL from our Delta Hedging model. Our objective is to calculate PnL at option expiry for the option writer. Primary contributors to the model include:

Figure 3 Delta Hedge – Cash P&L for the writer for an option that expires out of money
a) Cash in – receipts from the customer. Include premium received and the strike price if the option is exercised. If the option expires worthless we only receive the premium.
b) Cash out. As explained earlier to finance our hedge purchases we borrow money. We pay interest on this principal for the life of the hedge and return the principal at maturity.
c) Trading losses. As part of our strategy we purchase the underlying as prices rise and sell it when they fall. Be definition this strategy will generate trading losses irrespective of whether the option expires worthless or in the money. Because we re-balance on a frequent basis, trading losses also consume cash. However the question that often confuses audiences is one of double count. Should trading losses be included as a separate accounting item or are they already included in the Cash before trading losses calculation? Think about this before you proceed further. It will directly impact your analysis and result. Here is a hint – other than the cash treatment that we have used, is there any other possible use or source of cash in the analysis and the calculation above?
When we put the model in place our final output should look something like this:

Figure 4 Delta Hedge P&L Simulation results – Gross P&L, Net P&L, Trading Losses
You can clearly see that the biggest contributor to our cash PnL uncertainty is trading loss. Is this treatment correct?
We will take a more closer look at this contributor later in our note.
Extending the Delta Hedge Model for Cash PnL Calculation – Interest paid & principal borrowed for the Hedge
The first step is to add two new columns to our Delta hedge model. These are:
- Interest paid per period, and
- Incremental amount borrowed per period
Both elements have been calculated as part of the original sheet and all we need to do is simply extract the relevant piece and dump the results in two new columns at the end.
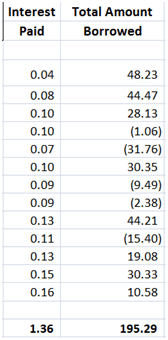
Figure 5 Delta Hedging PnL – Two new columns – Interest paid & Marginal borrowing
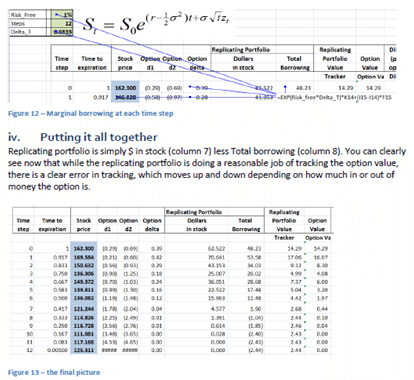
Incremental amount borrowed is included in the total borrowing figure we had calculated earlier in the Guide to delta hedging using Monte Carlo Simulation
post. It is simply the difference between the two deltas for the two time periods multiplied by the new price of the underlying stock.
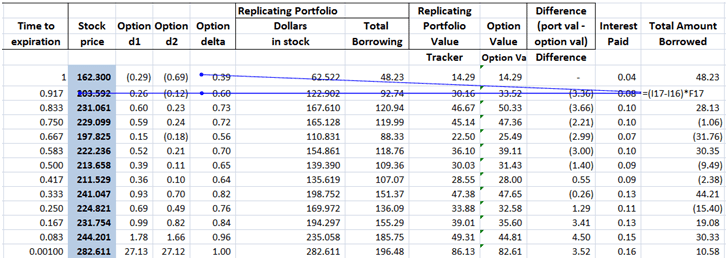
Figure 6 Delta Hedging PnL – Calculating Incremental borrowing
Interest paid per period is the interest accrued on the balance of the previous period. Which ends up as outstanding balance times the interest accrual factor (exp(risk_free_rate x Delta_T)) in the sheet.
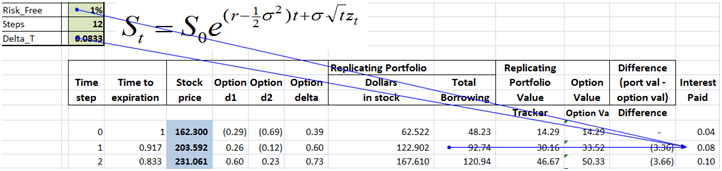
Figure 7 Delta hedging PnL – Calculating Interest paid on borrowed cash
Delta Hedging PnL – Calculating the trading loss on account of selling low
The basic hedging strategy is to buy when delta (or price) goes up and sell when delta (or price) goes down. Buy when prices rise, sell when they decline. The result is that as the underlying price see-saws, we end up buying high and selling low, rebalancing the portfolio in alignment with delta but also generating trading losses.
Our calculation of trading losses has three components.
a) First calculate the number of incremental units purchased or sold as part of the required rebalancing. (Unit purchased column)
b) Then calculate the difference in price between the two rebalancing periods. (Difference in price column)
c) Finally identify all trades where a sale was made and calculate the trading gain or loss. (Loss on Sale column)
For this specific simulation the trading loss is calculated as $2.5 based on the above approach.
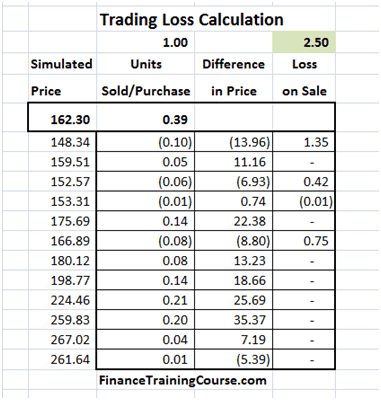
Figure 8 Delta Hedge simlation – trading loss calculation
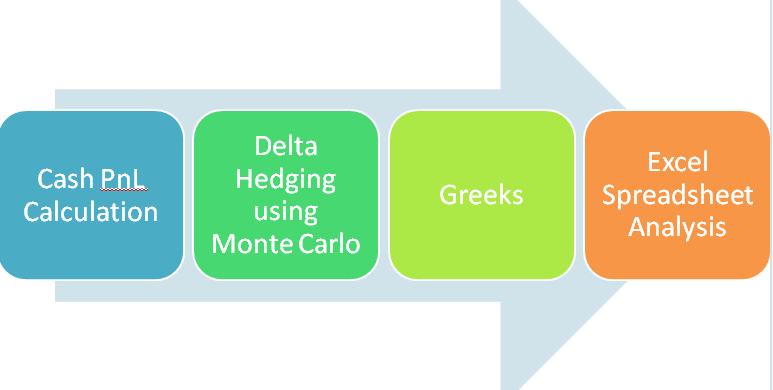
Delta Hedge PnL Calculation – Putting it all together
Now that we have all of the required PnL components together we hook them up with our Excel Data Table. We use our Monte Carlo bag of tricks to store the results of 100 iterations. Stored components include Gross PnL (excluding trading losses), Net PnL (including trading losses), Interest Paid & Trading loss on rebalancing sales.
But there is a trick question here. Its the question that has always stumped students (and quite frequently me). Here is the question. Is the correct P&L the Gross P&L or the Net P&L figure below? The net P&L subtracts the trading loss from the gross figure. Is that a double count? How would you explain and justify the answer? Is there a one word answer?
Think about these questions as you work through the numbers in the table below. We will do a post answering the double count question later. In the interim period here is a hint. Try a fully funded (zero premium) strategy once you have built the sheet and see what happens to your P&L calculation.
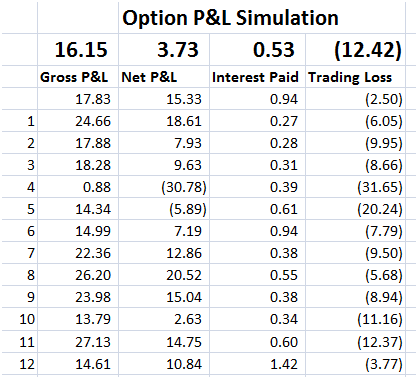
Figure 9 Delta Hedge PnL – Storing the results
(If this doesn’t make sense, take a quick look at our Monte Carlo Simulation refresher below.)
The final result is our Delta Hedge PnL graph for a European Call Option.

Figure 10 Dynamic Delta hedge PnL Calculation – PnL Graph
Delta hedging PnL – Next steps and Questions
Once you have the basic model figured out here are some interesting questions that follow:
a) How would you extend this model for PnL calculations for a European Put Option?
b) How would you incorporate the impact of implied volatility?
c) Of transaction costs? And non-risk free interest rates? Jumps and Dividends?
d) How would profitability (cash PnL) change if you shortened the time step and the rebalancing period? Or extended it?
e) What does the distribution of profits suggests about the risk inherent in the underlying business?
f) Is this the most effective way of hedging options?
g) What about the risk embedded in other Greeks? How is that managed and hedged? How does that impact PnL?
Related posts:
Long billed Hoopoe or a Crowned Woodpecker? You decide
Long billed Hoopoe or a crowned woodpecker?
A well rounded education in Finance includes an awareness of the environment around you.
This long billed bird has been prospecting in our office lawn for the last few months. Armed with our Kite catching camera, we took a few sneak shots early this afternoon. The only question is that are we looking at a long billed Hoopoe (probably) or a strange woodpecker (unlikely)?. Lacking expertise in the accurate classification of this species, we thought it would be appropriate to simply post the question here and hope for the best. Hope that some where in the audience there is a Quant who has been watching birds more closely than his Excel spreadsheets.
Long billed Hoopoe or a Woodpecker? You decide. (Need some help, check out the Woodpecker classification resource)
Side profile.
In action after a digging attempt is successful.
A full view of the crown on top from back
Getting ready to dig.
No related posts.