Fixed Income Investment Portfolio Management using duration, convexity and Excel solver
It doesn’t matter if you manage a pension fund, a life insurance trust fund or the proprietary book of an investment bank, at some point in time you hit your allocation and risk limits and need to rebalance your portfolio.
In most instances your limits and target accounts focus on interest rate sensitivity, volatility, Yield to risk ratios, liquidity and concentration limits. Your objective is to create the most efficient fixed income investment portfolio that balances an optimal mix of the above constraints against yield to maturity. The time tested, risk versus reward tweak.
In our new risk training workshop for fixed income portfolios case study we will build a simple model using Excel solver that shows how to handle the fixed income portfolio optimization problem. The model can be easily extended to handle larger portfolios and additional constraints around liquidity, factor sensitivity, volume concentration, value at risk and volatility.
For the purpose of this case study we will assume that we are advising a large pension fund who is re-evaluating fixed income portfolio allocation due to its new investment policy. The assets under management at the fund are US$500 million. We want to recommend:
- Portfolio allocation that minimizes duration
- Portfolio allocation that maximizes convexity
The liabilities are also equal to $500 million with a weighted average maturity of 20 years. Modified duration or interest rate sensitivity of liabilities was last measured in the monthly risk report at 9%.
Fixed Income Portfolio Management: Introducing Duration and Convexity
Duration is a measure of how prices of interest sensitive securities change as the underlying rate of interest changes. For example, if duration of a security works out to 2 this means roughly that for a 1% increase in interest rates price of the instrument will decrease by 2%. Similarly, if interest rates were to decrease by 1% the price of the security would rise by 2%.
Here is the numerical approximation for modified duration.
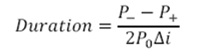
Figure 1 Fixed Income Portfolio management. Numerical approximation for duration
Convexity: The Duration approximation of change in price due to changes in the yield works only for small changes. For larger changes there will be a significant error term between the actual price change and that estimated change using duration.
Convexity improves on this approximation by taking into account the curvature of the price/ yield relationship as well as the direction of the change in yield. By doing so it explains the change in price that is not explained by Duration.
A positive convexity measure indicates a greater price increase when interest rates fall by a given percentage relative to the price decline if interest rates were to rise by that same percentage. A negative convexity measure indicates that the price decline will be greater than the price gain for the same percentage change in yield.
Duration and Convexity together are used to immunize a portfolio of assets and liability against interest rate shock.
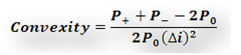
Figure 2 Fixed Income Portfolio Management. Numerical approximation for Convexity
Fixed Income Portfolio Management: Introducing the Optimization model
Our first scenario assumes a rising interest rate outlook. Ignoring liabilities and maturity mismatch for now, our fund manager would like to rebalance the portfolio to minimize duration so that the value of assets do not fall significantly due to changes in interest rates. We assume:
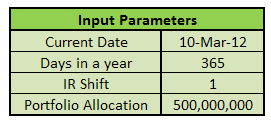
Figure 3 – Fixed Income Investment Portfolio – Date, Rate shift, size.
Fixed Income Investment Portfolio Management: Breaking down the optimization model
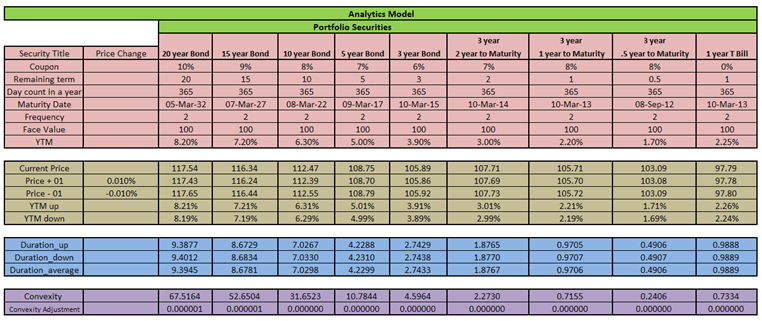
Figure 2 – Fixed Income Investment Portfolio Management: The securities analytics model
There are four parts to this model:
- Part 1- The securities universe specification: This is the pink-shaded area and defines the complete investment universe. You can only allocate a security if it is described in universe. Assets are classified in buckets of 20, 15, 10, 5 and 3 year maturities. We have assumed that current date (the valuation date) is the same as date of purchase (the settlement or value date) for all assets in all buckets.
-
Part 2 – The securities pricing model: This calculates the price and yield and is shaded brown. Current price is calculated using the Excel price function as illustrated below:
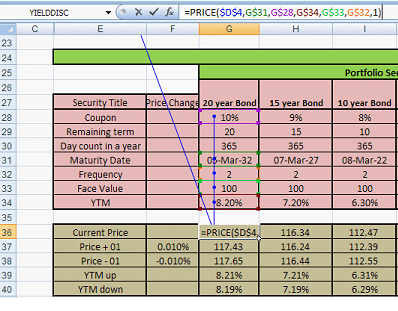
Figure 3 – Price calculation
The excel price (bond pricing) function is based on the data inputs of settlement date, date of maturity, coupon rate, yield to maturity, frequency and basis. Frequency here is 2 which mean that coupons are paid semi-annually. Cell $D$4 is the current date used in the input parameters in Figure 1.
Price changes just add or subtract the specified interest rate shocks and recalculate new prices for use in duration and convexity calculations. The rate shocks are 1 basis points (1/10,000).
-
Part 3 – Portfolio Duration Calculation: this is shaded blue and shows duration calculations. Duration is calculated using the duration approximation formula introduced above:
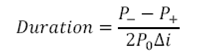
Figure 4 Fixed Income Investment Portfolio: Duration approximation
In the context of the Analytics Model, this is calculated as follows:
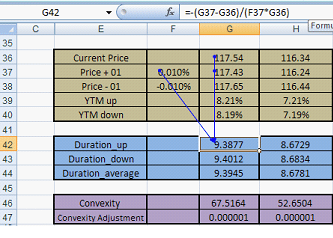
Figure 4 – Duration calculation
In calculation of Duration-down, Cell G44 is replaced by G45 and F44 is replaced by F45. Note that the general form of the formula is applied but instead of just calculating duration in one line, duration up and down are calculated respectively and the average of both is taken.
This average of the two durations will be used in our model. - Part 4 – Portfolio Convexity Calculation
-
The final part of the model calculates convexity and is highlighted in purple. The applicable convexity formula is:
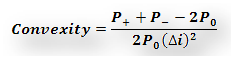
Figure 5 Fixed Income Portfolio Investment – Convexity calculation
The calculation is as under:
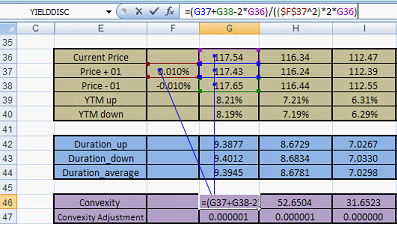
Figure 5 – Convexity calculation
The convexity adjustment is calculated using the formula:

Fixed Income Investment Portfolio Management: Summarized Portfolio Analytics
We now need a summarized portfolio analytics table that can be used in our optimization process. The results derived by combining the actual portfolio allocation and the portfolio analytics generated above would appear as shown below:
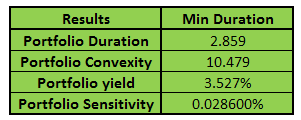
Figure 6 – Fixed Income Investment portfolio management. Portfolio analytics results
How are these results calculated? The answer is through the Analytics Model and the allocation of assets followed currently for each bucket. The allocation table is shown below:

Figure 7 – Portfolio allocation
Notice that the total bond portfolio allocation is 97% not 100%. 3% of the allocation is held in cash and/or non-interest sensitive securities.
Portfolio Duration is calculated by using the Excel sum-product function.
Sum-product is simply the combination of two operation that involves multiplying the individual cells in two vectors (Portfolio Allocation, Security Duration) and then summing the resulting product across all cells.
For instance (10%*duration average for 15 year bond) + (10%*duration average for 10 year bond)….. And so on.
Portfolio Convexity is calculated in the same manner by using the Excel sum-product function. (10%*convexity for 15 year bond) + (10%*convexity for 10 year bond)….. And so on.
And ditto for portfolio yield calculations. (10%*portfolio yield for 15 year bond) + (10%*portfolio yield for 10 year bond)….. And so on.
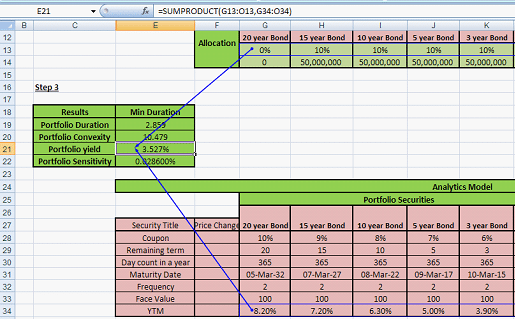
Figure 8 – Fixed Income Investment Portfolio Management: Calculating portfolio yield, portfolio duration and portfolio convexity
Portfolio sensitivity of -0.028600% is calculated in the following way:
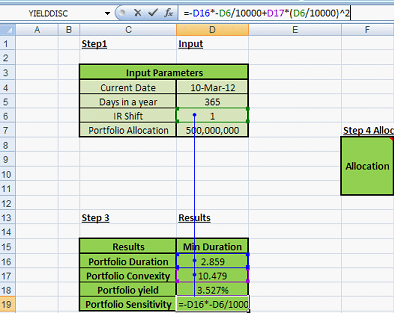
Figure 9 – Fixed Income Investments Portfolio Management. Calculating portfolio sensitivity
IR shift is the interest rate shift. It is measured in bps (basis point shift).
Fixed Income Investments Portfolio Management: Portfolio Optimization using solver
If we had a single linear equation representing a single constraint and a single position, the Excel Goal seek function would be sufficient. However a multi position fixed income investment portfolio has many constraints and many positions. In addition because you are dealing with bonds, the underlying model is no longer linear. You need a non-linear tweak to make it work.
The Excel solver function helps us optimize our portfolio allocation model with a few tweaks. We demonstrate the simplest of scenario in this write up but they can very easily be extended. As is the case with all optimization models, the trick is in designing the constraints. While there can be only one objective function (minimize or maximize a specific portfolio metric), with the right constraint design you could get close to a near optimal solution reasonably quickly. While the current model focuses only on fixed income investment portfolio, the design of the model can very easily be extended to multi-class portfolios. In addition new target accounts and risk constraints can be added just as easily.
Fixed Income Investments Portfolio Optimization. Optimizing the base case – Minimizing duration
The trustees of our pension fund have given a target to the investment fund manager to earn at least 3%. Bond proportion should be 99% of the fund, with the remaining for cash. Risk management and diversification targets specify that no greater than 13% of the total fund be allocated to any given asset bucket.
Given these objectives, how should the investment manager set out to minimize duration?
The targets are effectively constraints. Once we have defined them correctly, the solver function takes these constraints into account, evaluates the target optimization cell (minimize duration), and searches for an optimal solution. Since the layout of the spreadsheet has been described above, all we know need to do is to define the solver model and click solve.
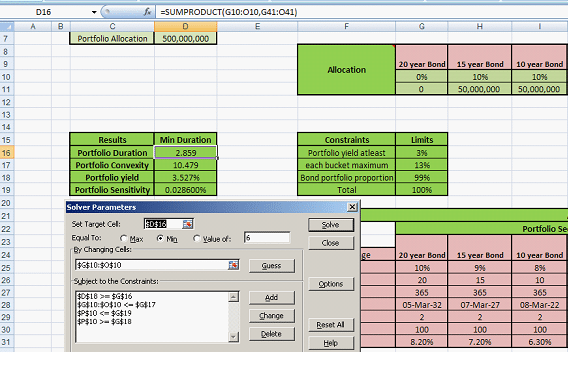
Figure 10 – Fixed Income Investments Portfolio Management. Using Excel Solver for minimizing duration for a fixed income portfolio
Pick ‘Min’ as your objective and then click ‘Solve’. Solver will work through the model till it reaches the optimal solution. The revised fixed income portfolio allocation is as follows:

Figure 11 – Portfolio allocation
Note that none of the asset bucket has higher than 13% proportion of assets. Also 99% is invested in bonds, rest in cash. The revised portfolio analytics summarizing our target account is also shown below:
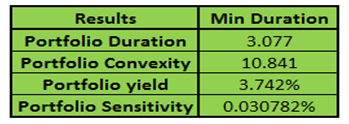
Figure 12 – Fixed income investments portfolio management – Revised portfolio analytics
Fixed Income Investments Portfolio Optimization – Maximizing Convexity
Positive convexity is generally a desirable attribute in a portfolio. In addition to minimizing duration, an alternate case could be made for maximizing convexity. If you expect rates to decline, a more convex fixed rate asset would rise by more compared to a less convex asset.
All it will take is set the Target Cell at portfolio convexity instead of duration. Note that in solver we click on ‘max’ instead of ‘min’ this time. The revised allocation is as follows:

Figure 13 – Fixed Income Investments Portfolio Management – Revised optimal portfolio allocation for maximizing convexity
And the revised portfolio analytics results for both the maximized convexity and minimized duration scenarios are presented below:
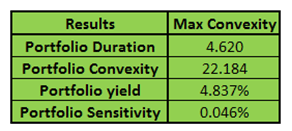
Figure 14 – Fixed Income Investment Portfolio Management – Optimized portfolio analytics results
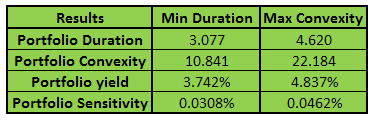
Figure 15 – Fixed Income Investments Portfolio Management – Consolidated results
Fixed Income Investments Portfolio Optimization. Next steps
You can easily extend the model to include constraints for value at risk, volatility, interest rate mismatch, gap management, concentration, portfolio liquidity, daily, monthly and weekly turnover, credit ratings and grades. A sample sheet showcasing some of these variations will be available for sale early next week at our store.
If you need more help beyond the sample portfolio, we also help customer build customized portfolio builds and solver models.
Related posts: