by ·Comments Off on Advance Risk Management Models – Workshop & Training reference page

Advance Risk Management Models – Free Online Resource Guide

Advance Risk Management Models (aka RM II) course is a 1 credit course taught at the SP Jain Campus in Dubai and Singapore by Jawwad Ahmed Farid.

A variation of this course was recently delivered (22-29th August 2012) at the SP Jain Dubai Campus by Jawwad. A smaller version of the course is scheduled for delivery at the Singapore campus in mid October 2012.

The course builds up on the work done in earlier MBA specialization courses (Risk Management I, Derivatives I and Derivatives II) conducted for regular and executive MBA students. The focus is on model building and practical applications using hands on models in Excel. The course reviews risk management models from the world of portfolio optimization, derivatives pricing and hedging, hedge optimization, banking regulation, credit risk, probability of default estimation.

Advance Risk Management Models – Course Prerequisites

Students are expected to be comfortable with materials covered in Risk Management I and the Derivatives I and II course series. See the reference site for Risk Management I for a quick review of risk management concepts. Without the relevant background you are likely to struggle so familiarity with the shared material is highly recommended.

Advance Risk Management Models – Course Plan

Here is the lesson plan for seven days of classes. The training workshop classes run for 150 minutes every day with homework assignments due for submission the next morning. As course material is documented and available for release the core theme links on this page (below) will be updated.

Advance Risk Management Models – Core Themes and study notes

  1. Fixed Income Value at Risk (VaR) Calculations for fixed rate bonds
  2. Fixed Income Investments Portfolio Optimization Model using Excel Solver
  3. Implied volatility, a simple introduction
  4. Delta Hedging introduction
  5. Delta Hedging European Calls and Put Contracts using Monte Carlo Simulation
  6. Option Greek Crash Course – Delta, Gamma, Vega, Theta & Rho
  7. A review of bank regulation and why it really doesn’t work.
  8. Basic credit analysis and models
  9. Probability of default calculations using the structured (Merton’s) approach
  10. Kill a bank in one day simulation – integrating funding, liquidity, ALM, credit allocation, capital adequacy and probabilty of shortfall.

Course note in the form of html posts are available for free. Downloadable pdf files and excel templates are available for purchase separately from our online store.

 

Related posts:

  1. Fixed Income Investment Portfolio Management & Optimization Case Study – Risk Training
  2. Financial Risk Management Workshop – Value at Risk, Volatility and Trailing correlations – Day One
  3. The Asset Liability and Liquidity Management Training Workshop, Subang Holiday Resort, Kula Lumpur, Malaysia, January 2011.

by ·Comments Off on Fixed Income Investment Portfolio Management & Optimization Case Study – Risk Training

Fixed Income Investment Portfolio Management using duration, convexity and Excel solver

It doesn’t matter if you manage a pension fund, a life insurance trust fund or the proprietary book of an investment bank, at some point in time you hit your allocation and risk limits and need to rebalance your portfolio.

In most instances your limits and target accounts focus on interest rate sensitivity, volatility, Yield to risk ratios, liquidity and concentration limits. Your objective is to create the most efficient fixed income investment portfolio that balances an optimal mix of the above constraints against yield to maturity. The time tested, risk versus reward tweak.

In our new risk training workshop for fixed income portfolios case study we will build a simple model using Excel solver that shows how to handle the fixed income portfolio optimization problem. The model can be easily extended to handle larger portfolios and additional constraints around liquidity, factor sensitivity, volume concentration, value at risk and volatility.

For the purpose of this case study we will assume that we are advising a large pension fund who is re-evaluating fixed income portfolio allocation due to its new investment policy. The assets under management at the fund are US$500 million. We want to recommend:

  • Portfolio allocation that minimizes duration
  • Portfolio allocation that maximizes convexity

The liabilities are also equal to $500 million with a weighted average maturity of 20 years. Modified duration or interest rate sensitivity of liabilities was last measured in the monthly risk report at 9%.

Fixed Income Portfolio Management: Introducing Duration and Convexity

Duration is a measure of how prices of interest sensitive securities change as the underlying rate of interest changes. For example, if duration of a security works out to 2 this means roughly that for a 1% increase in interest rates price of the instrument will decrease by 2%. Similarly, if interest rates were to decrease by 1% the price of the security would rise by 2%.

Here is the numerical approximation for modified duration.

Figure 1 Fixed Income Portfolio management. Numerical approximation for duration

Convexity: The Duration approximation of change in price due to changes in the yield works only for small changes. For larger changes there will be a significant error term between the actual price change and that estimated change using duration.

Convexity improves on this approximation by taking into account the curvature of the price/ yield relationship as well as the direction of the change in yield. By doing so it explains the change in price that is not explained by Duration.

A positive convexity measure indicates a greater price increase when interest rates fall by a given percentage relative to the price decline if interest rates were to rise by that same percentage. A negative convexity measure indicates that the price decline will be greater than the price gain for the same percentage change in yield.

Duration and Convexity together are used to immunize a portfolio of assets and liability against interest rate shock.

Figure 2 Fixed Income Portfolio Management. Numerical approximation for Convexity

Fixed Income Portfolio Management: Introducing the Optimization model

Our first scenario assumes a rising interest rate outlook. Ignoring liabilities and maturity mismatch for now, our fund manager would like to rebalance the portfolio to minimize duration so that the value of assets do not fall significantly due to changes in interest rates. We assume:


Figure 3 – Fixed Income Investment Portfolio – Date, Rate shift, size.

Fixed Income Investment Portfolio Management: Breaking down the optimization model


Figure 2 – Fixed Income Investment Portfolio Management: The securities analytics model

There are four parts to this model:

  • Part 1- The securities universe specification: This is the pink-shaded area and defines the complete investment universe. You can only allocate a security if it is described in universe. Assets are classified in buckets of 20, 15, 10, 5 and 3 year maturities. We have assumed that current date (the valuation date) is the same as date of purchase (the settlement or value date) for all assets in all buckets.
  • Part 2 – The securities pricing model: This calculates the price and yield and is shaded brown. Current price is calculated using the Excel price function as illustrated below:


    Figure 3 – Price calculation

     

    The excel price (bond pricing) function is based on the data inputs of settlement date, date of maturity, coupon rate, yield to maturity, frequency and basis. Frequency here is 2 which mean that coupons are paid semi-annually. Cell $D$4 is the current date used in the input parameters in Figure 1.

     

    Price changes just add or subtract the specified interest rate shocks and recalculate new prices for use in duration and convexity calculations. The rate shocks are 1 basis points (1/10,000).

     

  • Part 3 – Portfolio Duration Calculation: this is shaded blue and shows duration calculations. Duration is calculated using the duration approximation formula introduced above:

    Figure 4 Fixed Income Investment Portfolio: Duration approximation

    In the context of the Analytics Model, this is calculated as follows:

     

     

    Figure 4 – Duration calculation

     

    In calculation of Duration-down, Cell G44 is replaced by G45 and F44 is replaced by F45. Note that the general form of the formula is applied but instead of just calculating duration in one line, duration up and down are calculated respectively and the average of both is taken.
    This average of the two durations will be used in our model.

     

  • Part 4 – Portfolio Convexity Calculation
  • The final part of the model calculates convexity and is highlighted in purple. The applicable convexity formula is:

    Figure 5 Fixed Income Portfolio Investment – Convexity calculation

    The calculation is as under:

    Figure 5 – Convexity calculation

    The convexity adjustment is calculated using the formula:

     

    Fixed Income Investment Portfolio Management: Summarized Portfolio Analytics

     

    We now need a summarized portfolio analytics table that can be used in our optimization process. The results derived by combining the actual portfolio allocation and the portfolio analytics generated above would appear as shown below:

     


    Figure 6 – Fixed Income Investment portfolio management. Portfolio analytics results

    How are these results calculated? The answer is through the Analytics Model and the allocation of assets followed currently for each bucket. The allocation table is shown below:

     

 

Figure 7 – Portfolio allocation

Notice that the total bond portfolio allocation is 97% not 100%. 3% of the allocation is held in cash and/or non-interest sensitive securities.

Portfolio Duration is calculated by using the Excel sum-product function.

Sum-product is simply the combination of two operation that involves multiplying the individual cells in two vectors (Portfolio Allocation, Security Duration) and then summing the resulting product across all cells.

For instance (10%*duration average for 15 year bond) + (10%*duration average for 10 year bond)….. And so on.

Portfolio Convexity is calculated in the same manner by using the Excel sum-product function. (10%*convexity for 15 year bond) + (10%*convexity for 10 year bond)….. And so on.

And ditto for portfolio yield calculations. (10%*portfolio yield for 15 year bond) + (10%*portfolio yield for 10 year bond)….. And so on.

Figure 8 – Fixed Income Investment Portfolio Management: Calculating portfolio yield, portfolio duration and portfolio convexity

Portfolio sensitivity of -0.028600% is calculated in the following way:

Figure 9 – Fixed Income Investments Portfolio Management. Calculating portfolio sensitivity

IR shift is the interest rate shift. It is measured in bps (basis point shift).

Fixed Income Investments Portfolio Management: Portfolio Optimization using solver

If we had a single linear equation representing a single constraint and a single position, the Excel Goal seek function would be sufficient. However a multi position fixed income investment portfolio has many constraints and many positions. In addition because you are dealing with bonds, the underlying model is no longer linear. You need a non-linear tweak to make it work.

The Excel solver function helps us optimize our portfolio allocation model with a few tweaks. We demonstrate the simplest of scenario in this write up but they can very easily be extended. As is the case with all optimization models, the trick is in designing the constraints. While there can be only one objective function (minimize or maximize a specific portfolio metric), with the right constraint design you could get close to a near optimal solution reasonably quickly. While the current model focuses only on fixed income investment portfolio, the design of the model can very easily be extended to multi-class portfolios. In addition new target accounts and risk constraints can be added just as easily.

Fixed Income Investments Portfolio Optimization. Optimizing the base case – Minimizing duration

The trustees of our pension fund have given a target to the investment fund manager to earn at least 3%. Bond proportion should be 99% of the fund, with the remaining for cash. Risk management and diversification targets specify that no greater than 13% of the total fund be allocated to any given asset bucket.

Given these objectives, how should the investment manager set out to minimize duration?

The targets are effectively constraints. Once we have defined them correctly, the solver function takes these constraints into account, evaluates the target optimization cell (minimize duration), and searches for an optimal solution. Since the layout of the spreadsheet has been described above, all we know need to do is to define the solver model and click solve.

Figure 10 – Fixed Income Investments Portfolio Management. Using Excel Solver for minimizing duration for a fixed income portfolio

Pick ‘Min’ as your objective and then click ‘Solve’. Solver will work through the model till it reaches the optimal solution. The revised fixed income portfolio allocation is as follows:

Figure 11 – Portfolio allocation

Note that none of the asset bucket has higher than 13% proportion of assets. Also 99% is invested in bonds, rest in cash. The revised portfolio analytics summarizing our target account is also shown below:

Figure 12 – Fixed income investments portfolio management – Revised portfolio analytics

Fixed Income Investments Portfolio Optimization – Maximizing Convexity

Positive convexity is generally a desirable attribute in a portfolio. In addition to minimizing duration, an alternate case could be made for maximizing convexity. If you expect rates to decline, a more convex fixed rate asset would rise by more compared to a less convex asset.

All it will take is set the Target Cell at portfolio convexity instead of duration. Note that in solver we click on ‘max’ instead of ‘min’ this time. The revised allocation is as follows:

Figure 13 – Fixed Income Investments Portfolio Management – Revised optimal portfolio allocation for maximizing convexity

And the revised portfolio analytics results for both the maximized convexity and minimized duration scenarios are presented below:

Figure 14 – Fixed Income Investment Portfolio Management – Optimized portfolio analytics results

Figure 15 – Fixed Income Investments Portfolio Management – Consolidated results

Fixed Income Investments Portfolio Optimization. Next steps

You can easily extend the model to include constraints for value at risk, volatility, interest rate mismatch, gap management, concentration, portfolio liquidity, daily, monthly and weekly turnover, credit ratings and grades. A sample sheet showcasing some of these variations will be available for sale early next week at our store.

If you need more help beyond the sample portfolio, we also help customer build customized portfolio builds and solver models.

Related posts:

  1. Asset Liability Management Case Study: Understanding ALM using simple training cases
  2. Liquidity Risk Management Case Study: Lehman Brothers
  3. Liquidity Risk Management Case Study: American International Group (AIG): Timeline

by ·Comments Off on Sales & Trading Interview Guide: Understanding Greeks: Option Delta and Gamma

Sales & Trading Interview Guide: Understanding Greeks. Option Delta and Gamma.

Here is a short and sweet extract from the Sales & Trading Interview Guide series on Understanding Greeks (iBook and plain vanilla PDF version in the works). Rather than focus on formula and derivations, we have tried to focus on behavior. Our hope is the pretty pictures and colored graphs would help take some of the pain away from comprehending this topic.

Delta, Gamma, Vega, Theta & Rho. The five Greeks

There are five primary factor sensitivities that we are interested in when it comes to option pricing and derivative securities.

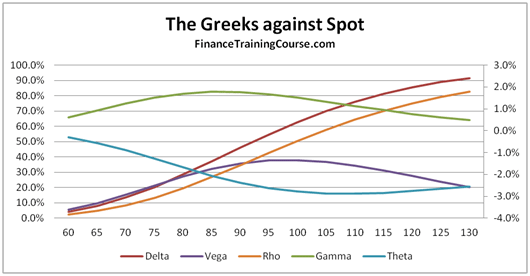
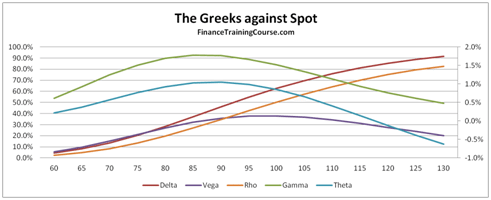
Figure 1 The Five Greeks. Plotted against changing spots

The image above presents a plot of the five factors for an At The Money (ATM) European call option.

Delta (Spot Price)- Measures the change in the value of the option price, based on a change in price of the underlying. Delta is the dark red line in the image above.

Vega (Volatility) – Measures the change in the value of the option price, based on a change in volatility of the underlying. Vega is the dark indigo line in the image above.

Rho (Interest Rates) – Measures the change in the value of the option price based on a change in interest rates.

Theta (Time to expiry) – Measures the change in the value of the option price based on a change in the time to expiry or maturity.

The first four sensitivities measure a change in the value of the option price based on a change in one of the determinants of option prices – spot price, volatility, interest rates and time to maturity. The fifth and final sensitivity is a little different. It doesn’t measure a change in option price, but measures a change in one of the sensitivities, based on a change in the price of the underlying.

Gamma – Measures a chance in the value of Delta, based on a change in the price of the underlying. If you are familiar with fixed income analytics, think of Gamma as Delta’s convexity.

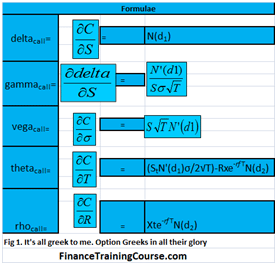
As promised above, we won’t hit you with any equations. However a quick notation summary is still required to appreciate the shape of the curves you are about to see.

Delta, Vega, Theta and Rho are all first order changes, while Gamma is second order change. If you take a quick look at the plot of the five factors presented above, you will see that the shape of the curves are similar for Delta and Rho (the slanting S) and similar for Gamma, Vega and Theta (the hill or inverted U). We will revisit the shape debate later on in our discussion.

Sales and Trading Interview Guide: Let’s talk about Delta

Delta has a handful of interpretations. Some common, some exotic.

The common interpretation is the one we have just covered above. Delta tracks option price sensitivity to changes in the price of the underlying. The second interpretation is as a conditional probability of terminal value (St) being greater than the Strike (X) given that St > X for a call option.

The third and the most relevant definition to our discussion comes from the option replicating and hedging portfolio example from the Black Scholes world.

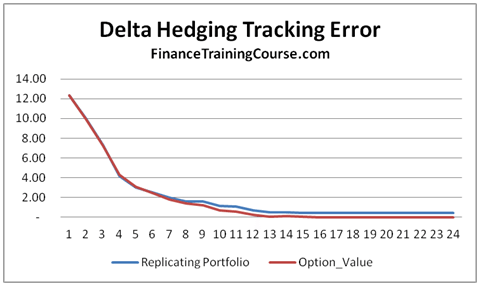
Figure 3 Delta Hedging. Replicating portfolio for call option using option Delta

As a seller of a call option if you would like to hedge your exposure (short call option) so that when (or if) the call option is actually exercised your loss is ideally completely offset by the change in value of your replicating portfolio.

This replicating portfolio is defined as a combination of two positions. A long position in the underlying given by Delta x S, less a borrowed amount.

Figure 4 – The Delta Hedge Relationship

For a European call option Delta is defined as

If we adjust Delta and with it the borrowing amount at suitably discrete time intervals we will find that our replicating portfolio will actually shadow or match the value of the option position. When the option is finally exercised (or not exercised) the two positions will offset each other.

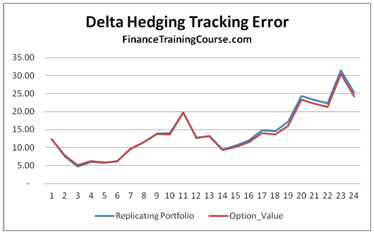
Figure 5 Delta Hedging. Replicating portfolio performance for hedging a short call option exposure

The two replications snap shots shown above show how closely the two portfolios move with changes in the underlying price over a one year time interval with fortnightly rebalancing (24 time steps). The tracking error will reduce if the rebalancing frequency is increased but it will also increase the cost of running the replicating portfolio.

Now that we have gotten the basic introduction out of the way, let’s spend some time on dissecting Delta by evaluating how this measure of option price sensitivity changes as you change:

a) Spot,

b) Strike,

c) Time to expiry and

d) Volatility.

Where relevant and important, we will add more context by also looking at how Delta’s behavior changes if the option is in, at, near or out of money.

Sales and Trading Interview Guide: Dissecting Delta – Against Spot

So how does Delta behave across a range of spot prices.

If we assume that we have purchased or sold a call option on a non-dividend paying stock with a strike price of US$100. The underlying is currently trading at a spot price of US$100. The time to expiry or maturity is one year.

Figure 6 Delta plotted against changing spot prices

The graph above shows the change in the value of Delta as spot prices move higher or lower from the original US$100.

In this specific instance while we have moved spot prices we have held maturity constant. As a result while spot prices for the underlying change from 60 to 130, the option’s delta doesn’t touch zero or 1, since there is a chance that it may still switch direction and go the other way.

How does the behavior of Delta change if you move across At money options to options that are deep out of money or deep in the money? Think about this for a second before you move forward. Would you expect to see a different curve? Or a different shape? How different?

Let’s start with at, in and near money options.

For at money or near money options the shape remains the same. For options that are deep in the money, it becomes asymptotic before finally touching 1. From our hedging definition above, this means that the seller of the option should now own the exact numbers of shares of the underlying committed to the call option (Delta = 1) since the option will most certainly expire in the money. From a probability definition perspective, for a call option a conditional probability of 1 indicates that the option is certain to expire in the money.

Figure 7 Delta against Spot. At, In and near money options

But what about deep out of money options? What happens to Delta or for that matter to all the other Greeks discussed earlier when it comes to deep out of money options.

We answer this question by plotting the Greeks for a European call option written with strike price of US$200, while the current spot price is only at US$100. In the price ranging between US$60 and US$130, the value of Delta touches zero and then slowly rises to about 8% as the underlying spot price reaches US$130.

The overall shape remains the same, all we are doing now is just looking at a different pane of the option sensitivity window. Slide a little further or put the two images (figure 7 and figure 8) side by side and you should be able to see the complete picture.

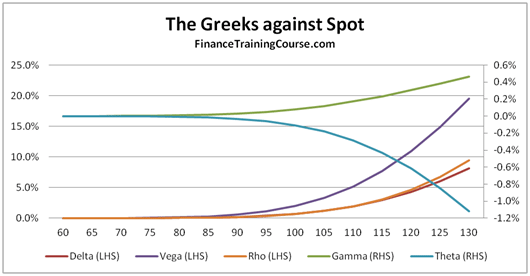
Figure 8 The Greeks against Spot. Deep out of money options

Figure 9 The Greeks against spot. AT, In and near money options

The next natural question deals with the valid range of values that Delta is expected to take. For a call option the range is between 0 and 1, as we have seen demonstrated above. Zero for deep out of money options, one for deep in money options. In between for all other shades.

For put options, Delta ranges between 0 and -1. Deep in money put options touch a Delta of -1, deep out of money put options reach a Delta of zero. The negative sign corresponds to a short position. To hedge a put, unlike a call, we short the underlying and invest the proceeds, rather than buy the underlying by borrowing the difference.

Sales and Trading Interview Guide: Dissecting Delta & Gamma – Against Strike

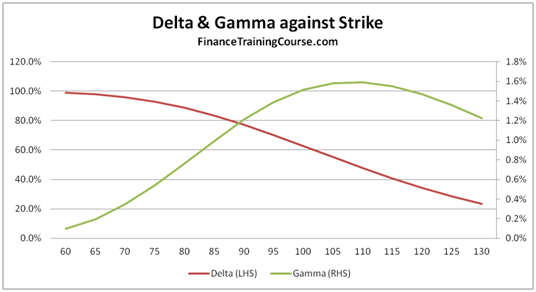
Figure 10 Delta & Gamma against changing strike price.

The next graph plots Delta and Gamma against changing strike price. We use a plot of both Delta and Gamma to reinforce the relationship between the two variables. Once again before you proceed further think about why do you see the two curves behave the way they do?

As the strike price moves to the right, the option gets deeper and deeper out of money. As it gets deeper in the deep out territory, the probability of its exercise and the amount required to hedge the exposure fall. Hence the steady decline in Delta as the strike price moves beyond the current spot price.

As the rate of change of Delta increases, we see Gamma rise by a proportionate amount. Gamma will only flatten out once the rate of change of Delta flattens out in the image above.

Sales and Trading Interview Guide: Dissecting Delta & Gamma – Against Time

The next three plots show how Delta and Gamma change as we vary time to expiry from a day to one year.

In the three snapshots that follow below, time moves from right to left (more to less). Once again we use both Delta and Gamma to reinforce the relationship between the two factors.

The only other variation from the options above is that we are now looking at three different options. An at money Call (Spot = 100, Strike = 100), an in money call (Spot = 110, Strike = 100) and a deep out of money call (Spot = 100, Strike = 200).

Notice how delta declines with time for an at money call, but rises to 1 for an in money call. Beyond a certain cut off point, it also rises for a deep out of money call but not as much as our first two pairs.

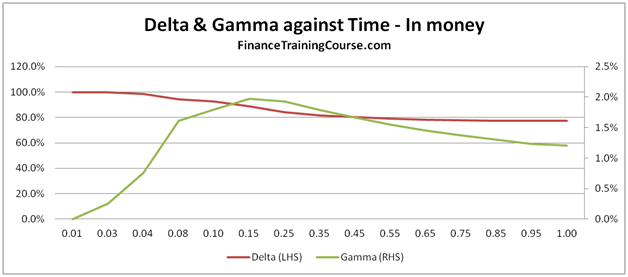
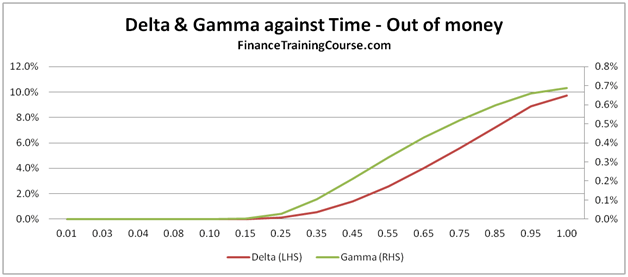
Figure 11 Delta & Gamm against Time for in, at and out of money options

Sales and Trading Interview Guide: Dissecting Delta & Gamma – Against Volatility

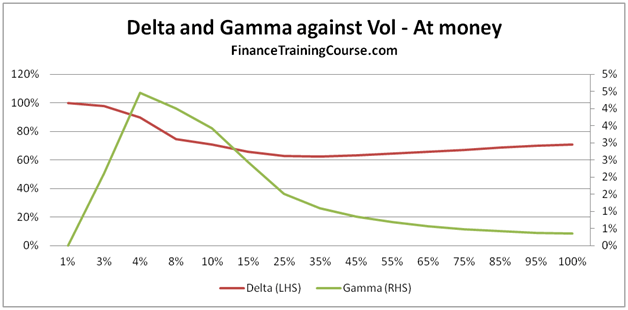
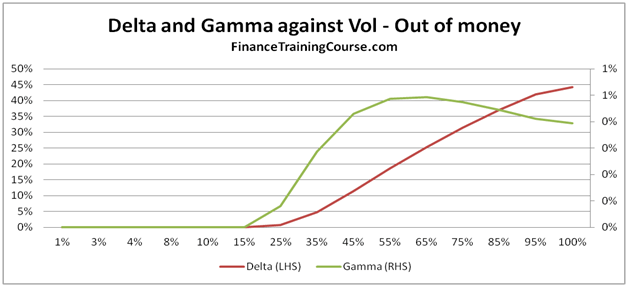
Figure 12 Delta, Gamma against Volatility. For at and out of money options.

For our last act, we plot Delta and Gamma against volatility and see a result which some students find counter intuitive.

For in, near or at money option, Delta actually falls with rising volatility. For most students this is a surprising result. Once would expect that with rising volatility, the value of the option should go up (correct) because the range of values reachable by the underlying is higher (also correct) hence leading to a higher probability of exercise (incorrect).

For deep out of money options, Delta rises with rising volatility. Gamma keeps pace initially but then runs out of steam as the rate of increase in Delta begins to flatten out.

To appreciate this behavior you actually have to move away from the Greeks and look at exercise probabilities.

Understanding the relationship between volatility, probability of exercise and price.

Our next three plots, show how the conditional probability of exercise N(d1), the unconditional probability of St > X, N(d1) and price behave and change for in, at and out of money European call options.

In the images beneath, Price is measured using the right hand scale, while the two probabilities are measured using the left hand scale.

For at, in and near money options, the two probabilities actually decline as volatility rise. Sounds counter intuitive when you consider that while the two probabilities are declining, the price of the option is actually rising.

Here is a hint, look up and think about volatility drag. For a deep out of money option the trend is reversed. Once again ask yourself why?

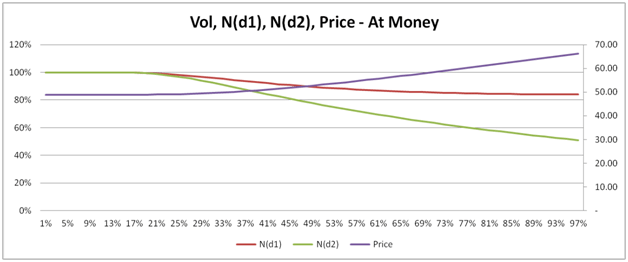
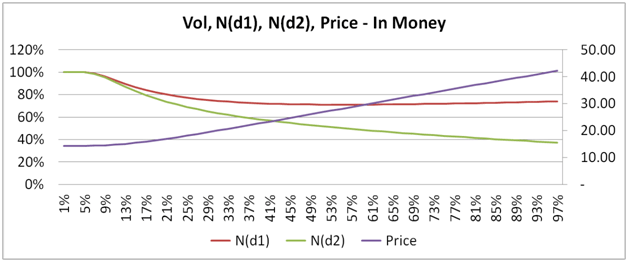
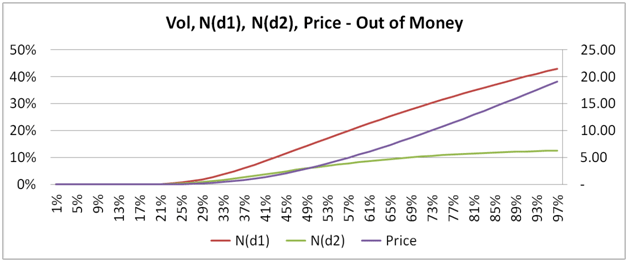
Figure 13 Vol, N(d1), N(d2) and Price for in, at, and deep out of money call options

Understanding Greeks: Option Delta and Gamma Review. Conclusion

If you are interested in a career on the floor or on a derivatives trading desk, you need to get very comfortable with the above graphs and behavior of Greeks across them. To the point of the lessons discussed becoming second nature – like riding a bike, breathing or drinking coffee. To remove the shock and awe caused by the partial differential equations behind the Greeks, we completely eliminated them from this post. In real life and when modeling them in excel you will have to get re-acquainted. Drop us a line with your questions or other dimensions that you would like us to address and if we can, we will do a few more posts on this topic.

Enjoy.

No related posts.

by ·Comments Off on Sales and Trading Interview Guide: Understanding Greeks – Preface

Sales and Trading Interview Guide: Understanding Greeks

Trading requires a combination of intuition, discipline and process. Of the three intuition is the most difficult to teach, since discipline and process is an incentives and control game. While individual intuition can be built over years of experience there are rules that make it easier to pick up that intuition faster.

Institutional intuition gets passed on between generation of traders through shadowing, standards, processes and controls. This passage of rites becomes easier if you have a knack for the subject, if you already know some of the rules or if you are familiar with the trading language.

The sales and trading language has many dimensions dealing with execution, trading strategy, customer behavior and product variations. This book only focuses on one very limited aspect of that language – the aspect dealing with risk management, hedging and Greeks.

The challenge with this part of the language lies partly with the terminology (a range of Greek symbols), partly with the presentation (partial differential equation), with calculations (a combination of Greek symbols and partial differential equations) and with interpretation (can you please say that again in a language that we can all understand).

Most business school derivative courses run out of time before the product universe has been covered, let alone spend time on teaching how to read, predict or forecast the behavior of exotic Greek symbols. .

Advance derivative courses cover pricing and if we are lucky spend limited time on sensitivities and Greeks because of conflicts with other topics in the outline. Sometime as business school students all we get are case notes and text references that are long on definitions and calculations but short on guidance and practical applications.

Which is unfortunate because the option price sensitivity topic is difficult to grasp for most audiences given its very non-linear nature. It takes time to think comfortably in the non-linear world. We understand simple straight forward, single dimensional relationships very well. When you ask us to envision a new dimension or even worse collate reactions from multiple dimensions into a single trading decision, our mental frameworks breakdown.

To develop an appreciation for this topic you need at least a few days of hands on or modeling experience followed by active application of the same concepts. The reason why you have purchased this book is because you don’t have a few days. You possibly have a few hours or a night before that interview or presentation is due.

So we have tried to compress primary lessons into short bite sized pieces. There are some equations but we don’t spend time on them or their derivations. We do spend time on ground rules, behavior and intuition. As a trader I am more likely to ask you about how Gamma is going to behave under a given scenario and how that is different from Vega’s reaction.

Our assumption is that you have some familiarity with Options, Black Scholes and the derivative pricing world. If this is not the case you need more help which is available on our partially free site at FinanceTrainingCourse.com

This book is based on a four part MBA course on derivative pricing and risk management that I have taught in Dubai and Singapore and the risk and treasury management practice I have run since 2003. The material is based on training tools we developed to teach advance treasury concepts to our students using our signature hands on, equations off mode.

And now let’s go waltz with some Greek symbols.

Related posts:

  1. The Sales and Trading Interview Guide Series – Understanding Greeks and Delta Hedging – Coming soon to an iPad near you…
  2. Investment Banking interview guide to Barclays Libor scandal
  3. US Credit Rating downgraded: Impact on commodities trading – outlook for the next week

by ·Comments Off on The Sales and Trading Interview Guide Series – Understanding Greeks and Delta Hedging – Coming soon to an iPad near you…

Preparing for the quantitative portion of a sales and trading interview for a main street bank is a nightmare. Specially if the bank is an active derivative trader and wants it intake class of interns and full time analysts and associates to hit the Sales and Trading desk running.

While basic option concepts generally get covered quite well in the MBA curriculum, when it comes to option price sensitivities and Greeks, our understanding remains rudimentary and superficial. One reason is the focus on formulas and calculation rather than intuition and understanding. Most courses have run out of time when it comes to delta, gamma, vega, theta and rho and stop after a basic rudimentary coverage of the material.

There is a lot of good material available on basic quantitative and numerical techniques tested in a Sales and Trading interview. But when it comes to option price sensitivities or Greeks, available material generally looks like this.

As part of the work we do with customers and students, our Apple iPad iBooks team is working on two very interesting and exciting titles.

The first is the Sales and Trading Interview Guide – Understanding Greeks for Dummies. Using the interactive iBook template we will help you master your Greeks to such a level where future mention of delta, gamma, vega, theta and rho would no longer break you out in cold sweat and palpitations. The iBook will cover Greeks behavior across time, volatility, spot and strike prices using easy to understand language, graphs and self assessment quizes.

But it’s the second iPad iBook title that we are really excited about. Sales and Trading Interview Guide – Delta Hedging and other higher dimensions, will help you build your own delta hedging sheet in excel using Monte Carlo Simulation. Both iPads books will have options for purchasing supporting excel spread sheets that extend the concepts covered in the iBook.

Planned for release in mid September, the two books will increase our inventory of interactive iBook for iPad titles to 5. Please feel free to drop me a note if you would like to learn more about the release dates and table of content for both titles.

Related posts:

  1. Asset Liability Management (ALM) Study Guide for Board Members – coming soon to an iPad near you.
  2. Understanding ALM and Calculating Value at Risk iBooks featured on the Apple iTunes store
  3. Accounting Crash Course: Small Business Accounting Training – Sales Journal and Sales Ledgers