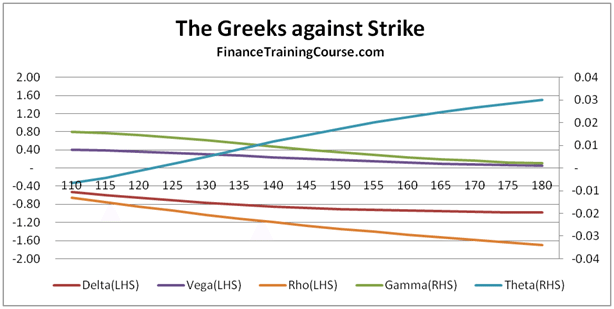
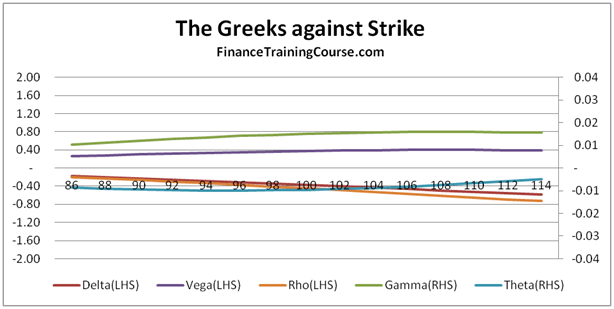
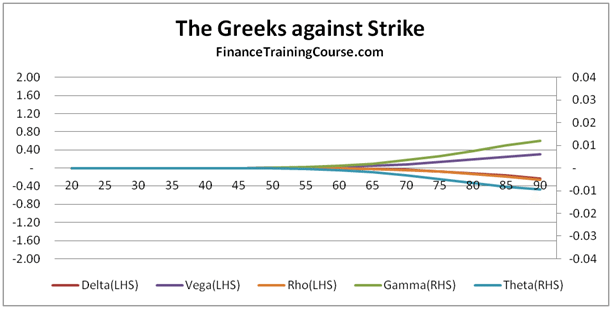
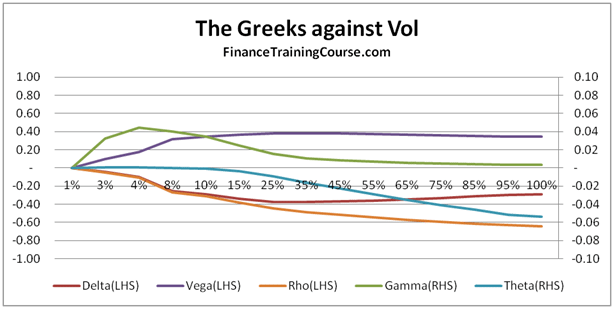
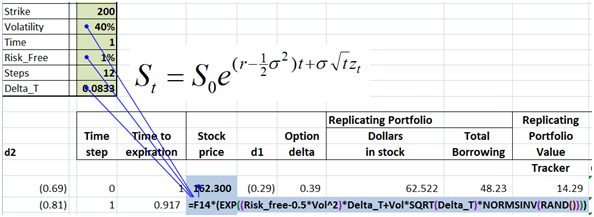Rebalancing frequency, Implied Volatility & Rho. Dynamic Delta Hedging Applications.
Now that we have a Delta Hedging Model for Calls and Puts let’s try and use it to answer the following questions:
a) What is the impact of rebalancing frequency on hedging profitability?
b) What is the impact of a rise in volatility on profitability? How does implied volatility help in interpreting this change?
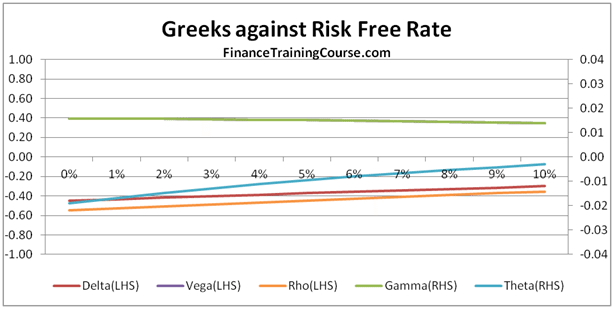
c) What is the impact of changes in risk free rates on profitability?
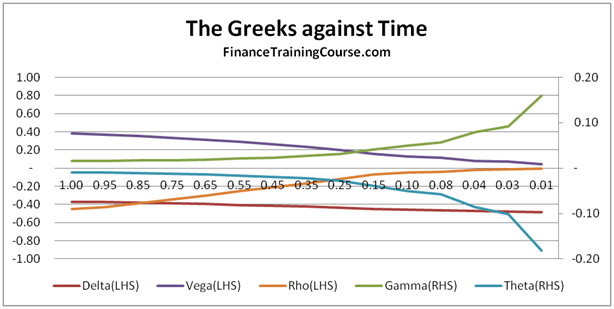
d) How does the interaction of time to expiry and volatility changes profitability?
These are all questions that should occur naturally to you as you spend more time with the Delta Hedging model. They are also essential to building a deeper understanding of the concept of implied volatility, Rho & Theta.
Dynamic Delta Hedging Questions: Assumptions & Securities
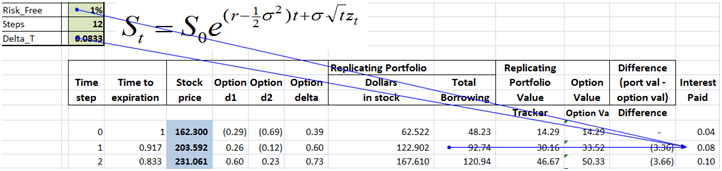
Let’s take a look at these questions one by one. We will begin work with a call option assuming the following valuation parameters:
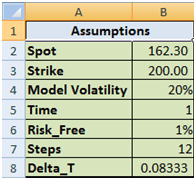
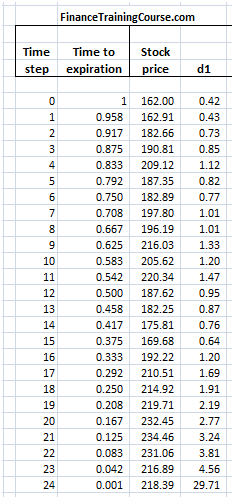
Figure 1 Dynamic Delta Hedging – P&L review assumptions
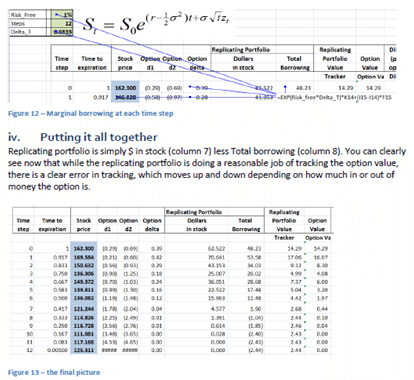
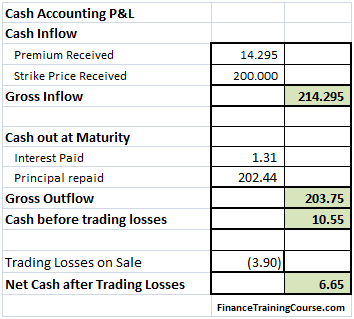
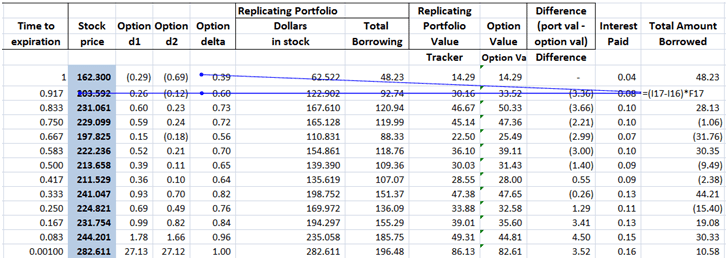
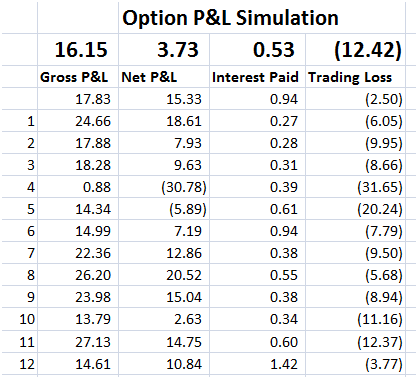
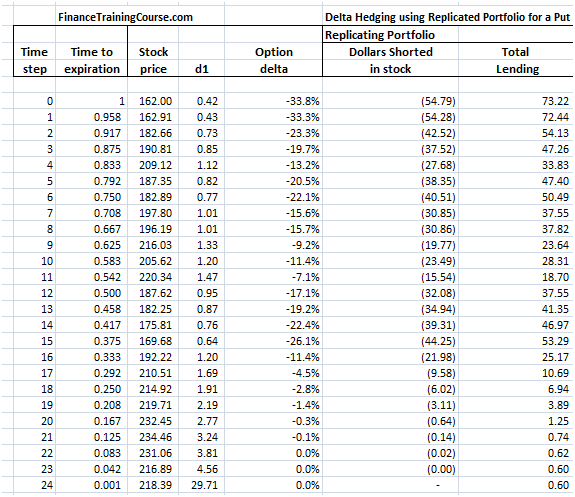
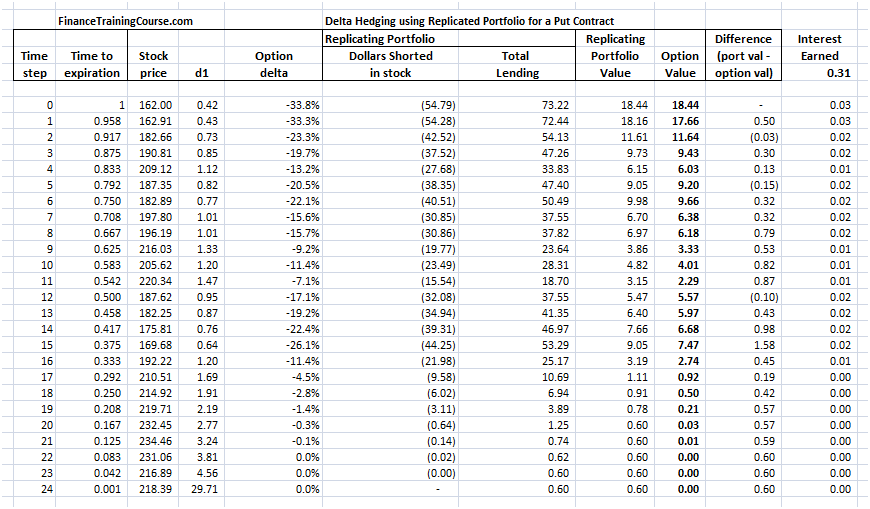
The theoretical value of the call option is 3.01 based on the above assumptions. The resulting Cash Accounting P&L for a single run of the Dynamic Delta Hedging model is as under:
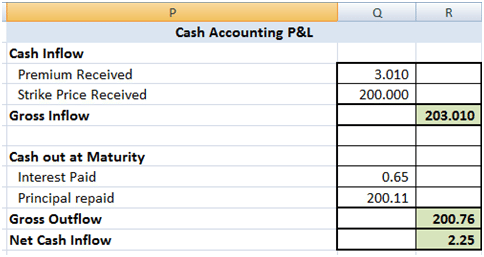
Figure 2 Dynamic Delta Hedging – P&L Review – Base case
Rebalancing frequency & efficiency of the hedge. Implications for profitability?
A good hedge is one where the cost of the hedge is close to the theoretical value of the option. In our cash accounting P&L we have included the theoretical premium received which is used in determining the initial amount to be borrowed. Hence for a hedge to be considered good or efficient the Net P&L should be close to this premium amount.
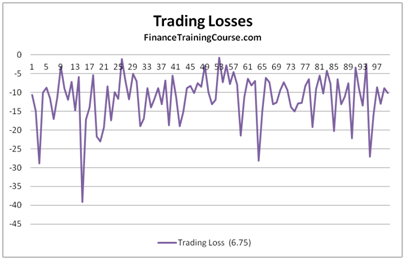
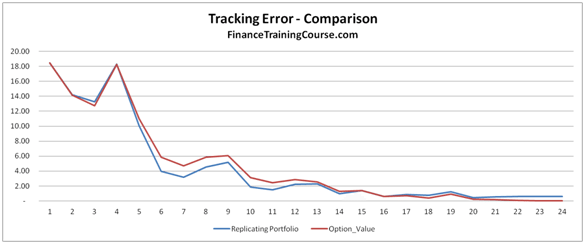
To see if increasing the frequency led to better results, we increase the time steps used from 12 steps to 365 steps. The graph below plots the Net P&L to Theoretical Value across 100 simulated runs. A value close to 100% means that it is a close match to the premium whereas a value farther away for 100% indicates a poor match.
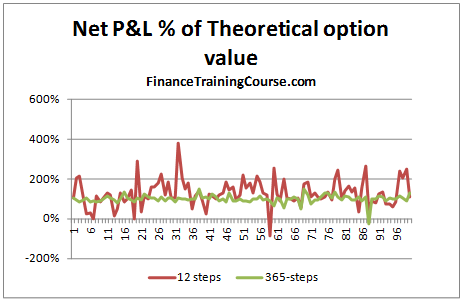
Figure 3 Dynamic Delta Hedging – P&L Simulation – Rebalancing frequency
We can clearly see that there is much greater variation when the rebalancing is done on a monthly basis than when it is carried out on a daily basis.
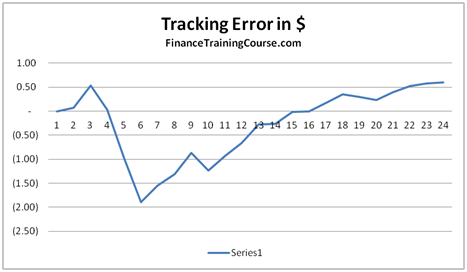
The graph below gives a similar picture. In this case however, the premium is not considered when determining the amount to be borrowed at option inception, i.e. the hedge is fully funded through borrowing. A value of -100% indicates that the Net P&L i.e. the cost of the hedge, in this case exactly matches the theoretical value of the call option.

Figure 4 Dynamic Delta Hedging – P&L Simulation – Hedge Effectiveness
But that is the risk manager’s point of view. What about a trader’s point of view?
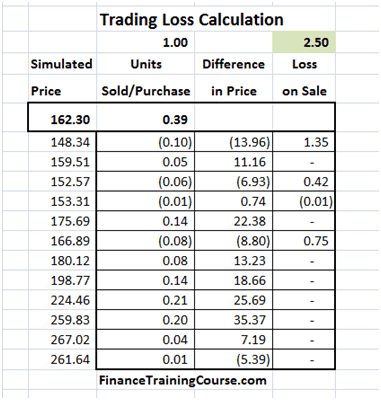
From a trading point of view there are two lessons here. First the large variation in P&L linked to jump’s in the underlying price is the un-hedged Gamma at work (Is that true? Think about it). Second would you prefer to limit the cost of hedging the option to the amount you have charged your customer or less? If you are in the business of earning a living from writing options, the premium you charge on the options you sell should always be higher than your cost; your cost of effectively hedging the option.
Now back to the Gamma question. Gamma is your second order error term. Conceptually it’s similar to convexity and linked to changes in not just the underlying price but also volatility. Is your true P&L (the premium received less the actual cost of hedging) is the summation of the hedge error?
Volatility and profitability. The question of implied volatility
With volatility there are multiple questions. How does profitability change when the general environment moves from low volatility to high volatility? How does profitability change when you have already written an option and volatility moves for or against you?
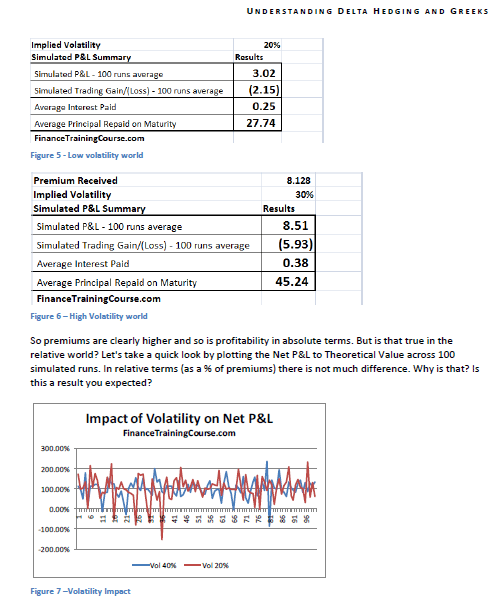
Let’s start from the first question. Using the 12-step model we calculate the impact on Net P&L. In our base case we have assumed a volatility of 20%. Let us now assume that the volatility increases to 40%. What is the impact on hedge efficiency for options written in the two different environment?

Figure 5 Volatility & Profitability – Low volatility world
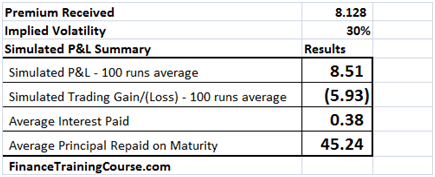
Figure 6 Volatility & Profitability – High Volatility world
So premiums are clearly higher and so is profitability in absolute terms. But is that true in the relative world? Let’s take a quick look by plotting the Net P&L to Theoretical Value across 100 simulated runs. In relative terms (as a % of premiums) there is not much difference. Why is that? Is this a result you expected?
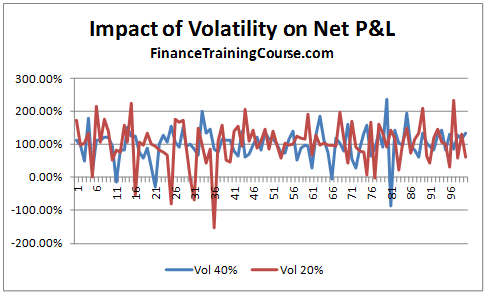
Figure 7 Dynamic Delta Hedging – P&L Simulation – Volatility Impact
To answer these questions you have to revisit implied volatility. Let’s use the same scenario as above but with a minor change. We wrote options and received premiums assuming an implied volatility of 30%. The actual realized volatility over the life of the option was 20%. How did that change our resulting simulated P&L.

Figure 8 Implied volatility at work – Hedge Profitability
You can now see a clear difference in absolute as well as relative terms in net P&L. And the difference arises on account of the spread between the premium charged ($8.13) versus the premium needed ($3.01).
(To run this exercise using the Delta Hedge Sheet, simply calculate the value of the premium at the implied volatility level you want to charge and replace the original premium in the simulation with this value).
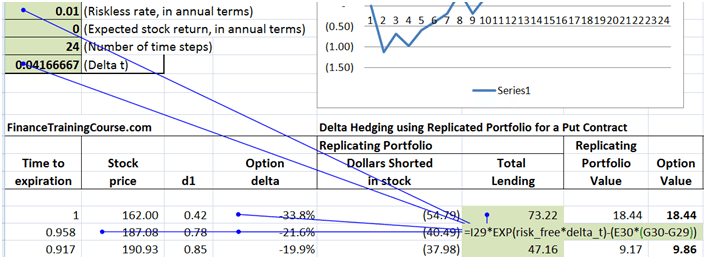
Risk free rates & profitability. The question of Rho.
We present the results of three P&L simulations runs in the tables below. The first assumes a risk free interest rate of 1%, the 2nd uses 2% and the third uses a risk free interest rate estimate of 5%.
The first two are easy, rates go up, premiums goes up and a European Call option becomes more expensive. Why is that?
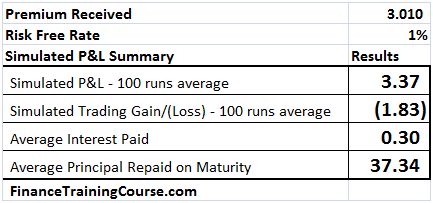
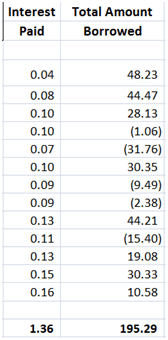
Figure 9 Dynamic Delta Hedging profitability – P&L at 1% interest rates
The reason is the average interest paid column. The premium goes up by 28 cents of which 21 cents is the increased cost of financing the borrowed position. Where does the other 7 cents comes from? (Need a hint – Other than the borrowing component who else benefits or uses r, the risk free rate?)
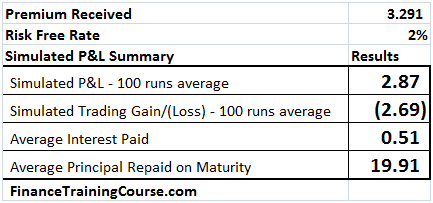
Figure 10 Dynamic Delta Hedging profitability – P&L at 2% interest rate
The second one is more difficult. In this instance as rates increase to 5% from the original 1%, the cost of borrowing balloons to $1.95 from the original $0.30 but the impact in option premium is only $1.244. How does this work? (Hint, think about what other driver/factor in the Black Scholes Analysis uses r?)

Figure 11 Dynamic Delta Hedging profitability – P&L at 5% interest rates
In addition to borrowing the difference between premium received and Delta hedge, the other usage of the risk free rate, r, is in estimating the future value of the underlying asset in the BSM (Black Scholes Model’s) risk neutral world. This implies that there are other components of Rho, in addition to the borrowing cost. That you need to examine and be comfortable with.

Related posts:
- Understanding Delta Hedging for options using Monte Carlo Simulation
- Dynamic Delta Hedging – Calculating Cash PnL (Profit & Loss) for a Call Option writer
- Dynamic Delta Hedging – Extending the Monte Carlo simulation model to Put contracts