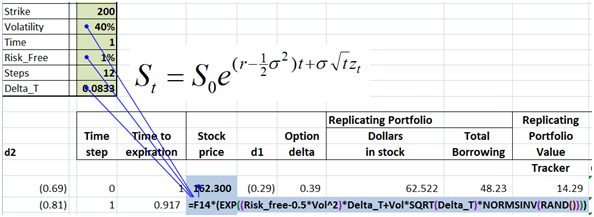Dynamic Delta Hedging – Calculating Cash PnL (P&L) for a European Call Option
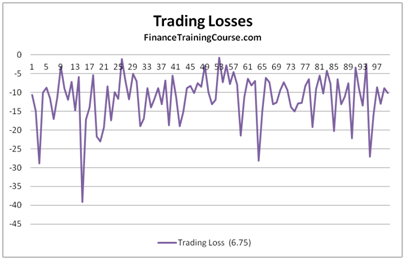
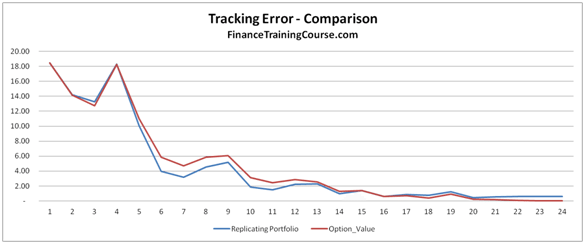
Figure 1 Delta Hedge P&L – Trading losses on account of rebalancing
We extend the original Dynamic Delta Hedging Monte Carlo Simulation spread sheet in this note. The dynamic hedging spreadsheet for a European call option allowed us to do a step by step trace of a delta hedging simulation. In this sheet we will use the results from the simulation trace to calculate a cash accounting P&L for our hedging model assuming the role of a call option writer and then extend the original simulation to see the average PnL across 100 iterations.
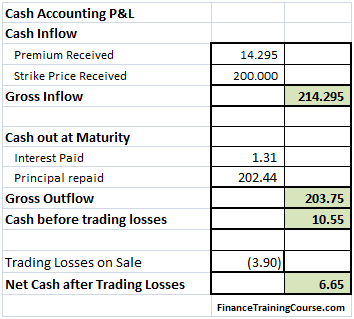
The above calculation has a double count in it? Which directly impacts the final profitability figure? Can you see it? See the discussion below for an answer.
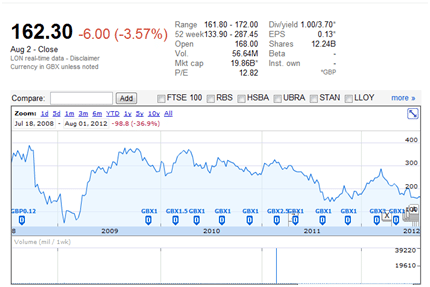
We are assuming that we have written a European call option on Barclays Bank where the current spot price is $162.3 and the strike price is US$200. Time to expiry is one year and Barclays Bank is unlikely to pay a dividend during the life of the option.
Figure 2 Delta Hedge P&L – Cash P&L for the writer for a call option that expires in the money
Understanding Delta Hedging Cash PnL Calculation – Required resources
Before you proceed further if you are still uncomfortable with option price sensitivities or delta hedging please use the following background and model review posts to make yourself comfortable with the underlying concepts.
- Understanding option Greeks reference resource for dummies
- Understanding Greeks – Analyzing Delta & Gamma
- Understanding Greeks – The Guide to delta hedging using Monte Carlo Simulation
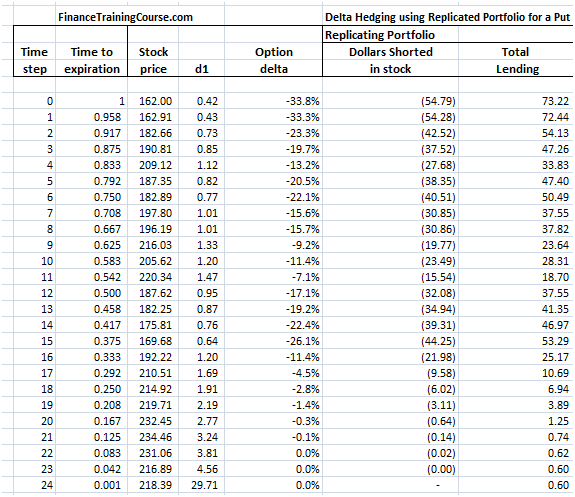
- Understanding Greeks – The Delta Hedging Simulation extended for Put Options
Delta Hedging Cash PnL Calculations – Dissecting the PnL Model
Our model uses a simplified cash based approach to calculate PnL from our Delta Hedging model. Our objective is to calculate PnL at option expiry for the option writer. Primary contributors to the model include:

Figure 3 Delta Hedge – Cash P&L for the writer for an option that expires out of money
a) Cash in – receipts from the customer. Include premium received and the strike price if the option is exercised. If the option expires worthless we only receive the premium.
b) Cash out. As explained earlier to finance our hedge purchases we borrow money. We pay interest on this principal for the life of the hedge and return the principal at maturity.
c) Trading losses. As part of our strategy we purchase the underlying as prices rise and sell it when they fall. Be definition this strategy will generate trading losses irrespective of whether the option expires worthless or in the money. Because we re-balance on a frequent basis, trading losses also consume cash. However the question that often confuses audiences is one of double count. Should trading losses be included as a separate accounting item or are they already included in the Cash before trading losses calculation? Think about this before you proceed further. It will directly impact your analysis and result. Here is a hint – other than the cash treatment that we have used, is there any other possible use or source of cash in the analysis and the calculation above?
When we put the model in place our final output should look something like this:

Figure 4 Delta Hedge P&L Simulation results – Gross P&L, Net P&L, Trading Losses
You can clearly see that the biggest contributor to our cash PnL uncertainty is trading loss. Is this treatment correct?
We will take a more closer look at this contributor later in our note.
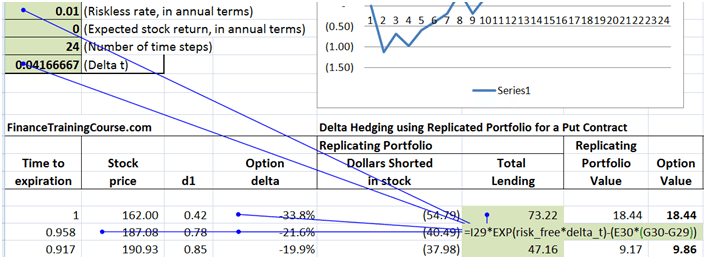
Extending the Delta Hedge Model for Cash PnL Calculation – Interest paid & principal borrowed for the Hedge
The first step is to add two new columns to our Delta hedge model. These are:
- Interest paid per period, and
- Incremental amount borrowed per period
Both elements have been calculated as part of the original sheet and all we need to do is simply extract the relevant piece and dump the results in two new columns at the end.
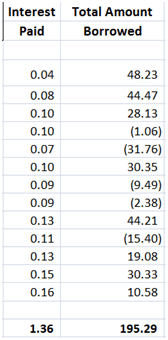
Figure 5 Delta Hedging PnL – Two new columns – Interest paid & Marginal borrowing
Incremental amount borrowed is included in the total borrowing figure we had calculated earlier in the Guide to delta hedging using Monte Carlo Simulation
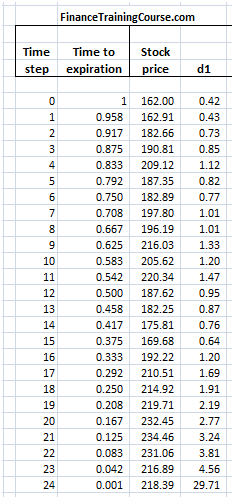
post. It is simply the difference between the two deltas for the two time periods multiplied by the new price of the underlying stock.
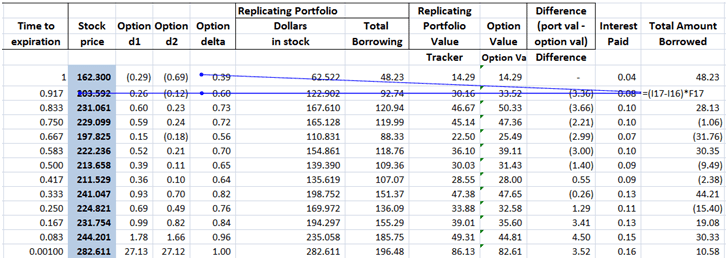
Figure 6 Delta Hedging PnL – Calculating Incremental borrowing
Interest paid per period is the interest accrued on the balance of the previous period. Which ends up as outstanding balance times the interest accrual factor (exp(risk_free_rate x Delta_T)) in the sheet.
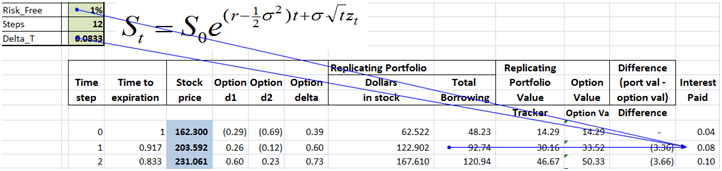
Figure 7 Delta hedging PnL – Calculating Interest paid on borrowed cash
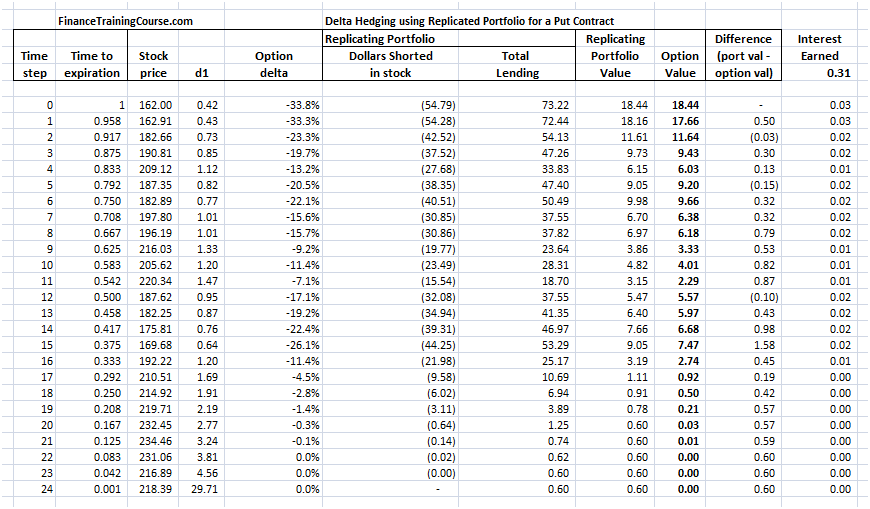
Delta Hedging PnL – Calculating the trading loss on account of selling low
The basic hedging strategy is to buy when delta (or price) goes up and sell when delta (or price) goes down. Buy when prices rise, sell when they decline. The result is that as the underlying price see-saws, we end up buying high and selling low, rebalancing the portfolio in alignment with delta but also generating trading losses.
Our calculation of trading losses has three components.
a) First calculate the number of incremental units purchased or sold as part of the required rebalancing. (Unit purchased column)
b) Then calculate the difference in price between the two rebalancing periods. (Difference in price column)
c) Finally identify all trades where a sale was made and calculate the trading gain or loss. (Loss on Sale column)
For this specific simulation the trading loss is calculated as $2.5 based on the above approach.
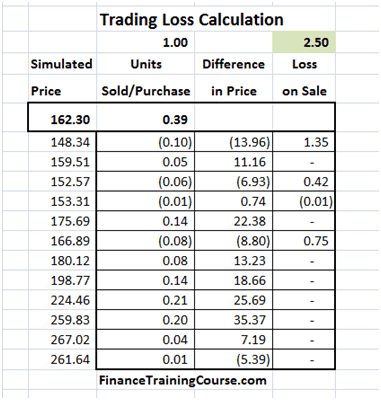
Figure 8 Delta Hedge simlation – trading loss calculation
Delta Hedge PnL Calculation – Putting it all together
Now that we have all of the required PnL components together we hook them up with our Excel Data Table. We use our Monte Carlo bag of tricks to store the results of 100 iterations. Stored components include Gross PnL (excluding trading losses), Net PnL (including trading losses), Interest Paid & Trading loss on rebalancing sales.
But there is a trick question here. Its the question that has always stumped students (and quite frequently me). Here is the question. Is the correct P&L the Gross P&L or the Net P&L figure below? The net P&L subtracts the trading loss from the gross figure. Is that a double count? How would you explain and justify the answer? Is there a one word answer?
Think about these questions as you work through the numbers in the table below. We will do a post answering the double count question later. In the interim period here is a hint. Try a fully funded (zero premium) strategy once you have built the sheet and see what happens to your P&L calculation.
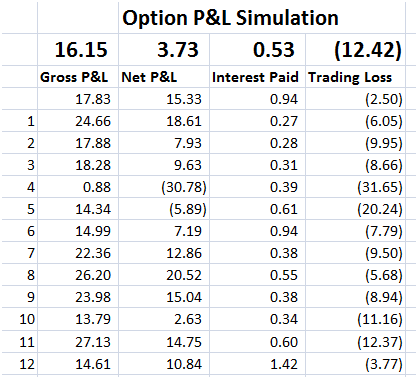
Figure 9 Delta Hedge PnL – Storing the results
(If this doesn’t make sense, take a quick look at our Monte Carlo Simulation refresher below.)
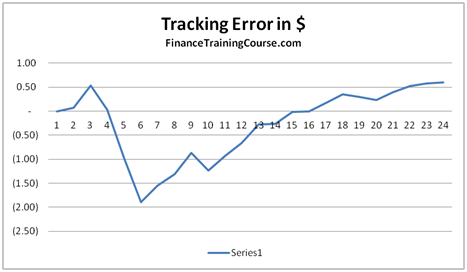
The final result is our Delta Hedge PnL graph for a European Call Option.

Figure 10 Dynamic Delta hedge PnL Calculation – PnL Graph
Delta hedging PnL – Next steps and Questions
Once you have the basic model figured out here are some interesting questions that follow:
a) How would you extend this model for PnL calculations for a European Put Option?
b) How would you incorporate the impact of implied volatility?
c) Of transaction costs? And non-risk free interest rates? Jumps and Dividends?
d) How would profitability (cash PnL) change if you shortened the time step and the rebalancing period? Or extended it?
e) What does the distribution of profits suggests about the risk inherent in the underlying business?
f) Is this the most effective way of hedging options?
g) What about the risk embedded in other Greeks? How is that managed and hedged? How does that impact PnL?
Related posts: